Câu 2:
\(P=\dfrac{-4cosx-3sinx}{3cosx+5sinx}\)
\(P=\dfrac{-4-3tanx}{3+5tanx}\) (chia cả tử và mẫu cho cosx)
Thay \(tanx=4\) vào \(P\) ta có:
\(P=\dfrac{-4-3.4}{3+5.4}\)\(=-0,70\)
Câu 4:
Gọi số hạng liên tiếp của cấp số cộng cần tìm là: \(x;\dfrac{x+y}{2};y\)
Theo đề bài tổng 3 số là 21 nên ta có:
\(x+\dfrac{x+y}{2}+y=21\)
\(\Rightarrow\dfrac{2x+x+y+2y}{2}=21\)
\(\Rightarrow3x+3y=42\)
\(\Rightarrow3.\left(x+y\right)=42\Rightarrow x+y=14\)
Nếu lấy số thứ hai trừ đi 1 và số thứ ba cộng thêm 1 thì ba số đó lập thành cấp số nhân nên ta có:
\(x.\left(y+1\right)=\left(\dfrac{x+y}{2}-1\right)^2\)
\(\Rightarrow xy+x=\left(\dfrac{x+y-2}{2}\right)^2\)
Thay y = 14-x vào pt trên ta có:
\(x\left(14-x\right)+x=\left(\dfrac{x+14-x-2}{2}\right)^2\)
\(\Rightarrow14x-x^2+x=6^2\)
\(\Rightarrow-x^2+15x-36=0\)
\(\Rightarrow\left(x-12\right).\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=12\left(l\right)\\x=3\left(c\right)\end{matrix}\right.\)
Vậy số hạng nhỏ hơn 4 là 3
Đúng 4
Bình luận (0)
Các câu hỏi tương tự
Giải giúp em câu bcdef với ạ riêng b,e,f giải đưa về cos giúp em

Giải Giúp em câu này với ạ. Em cảm ơn!
Giải giúp em câu b với, câu b thôi nha. Em cảm ơn nhiều ạ! 
 ai giải giúp em với ạ
ai giải giúp em với ạ
Mn giúp em giải và giải thích từng câu với ạ
Mn giúp em giải và giải thích từng câu với ạ
Mn giúp em giải và giải thích từng câu với ạ

Giải thích giúp em câu 2 với ạ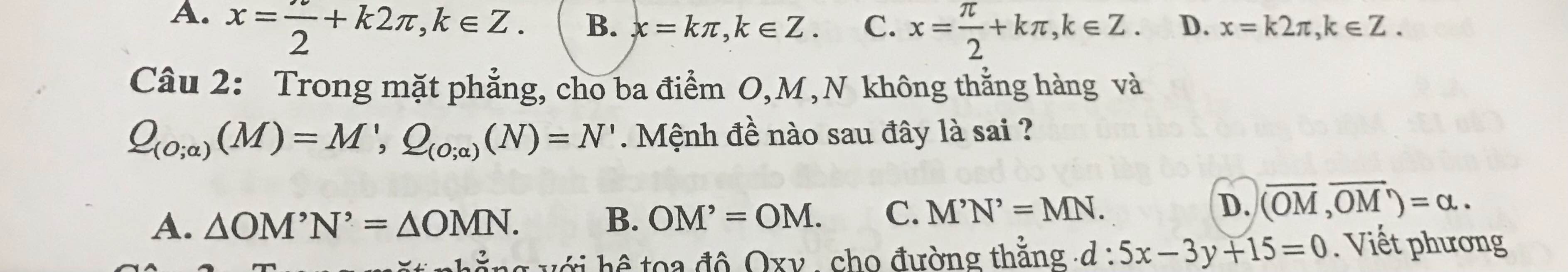
Giúp em giải tự luận câu 1 với ạ

Mọi người giải giúp em câu này với ạ











