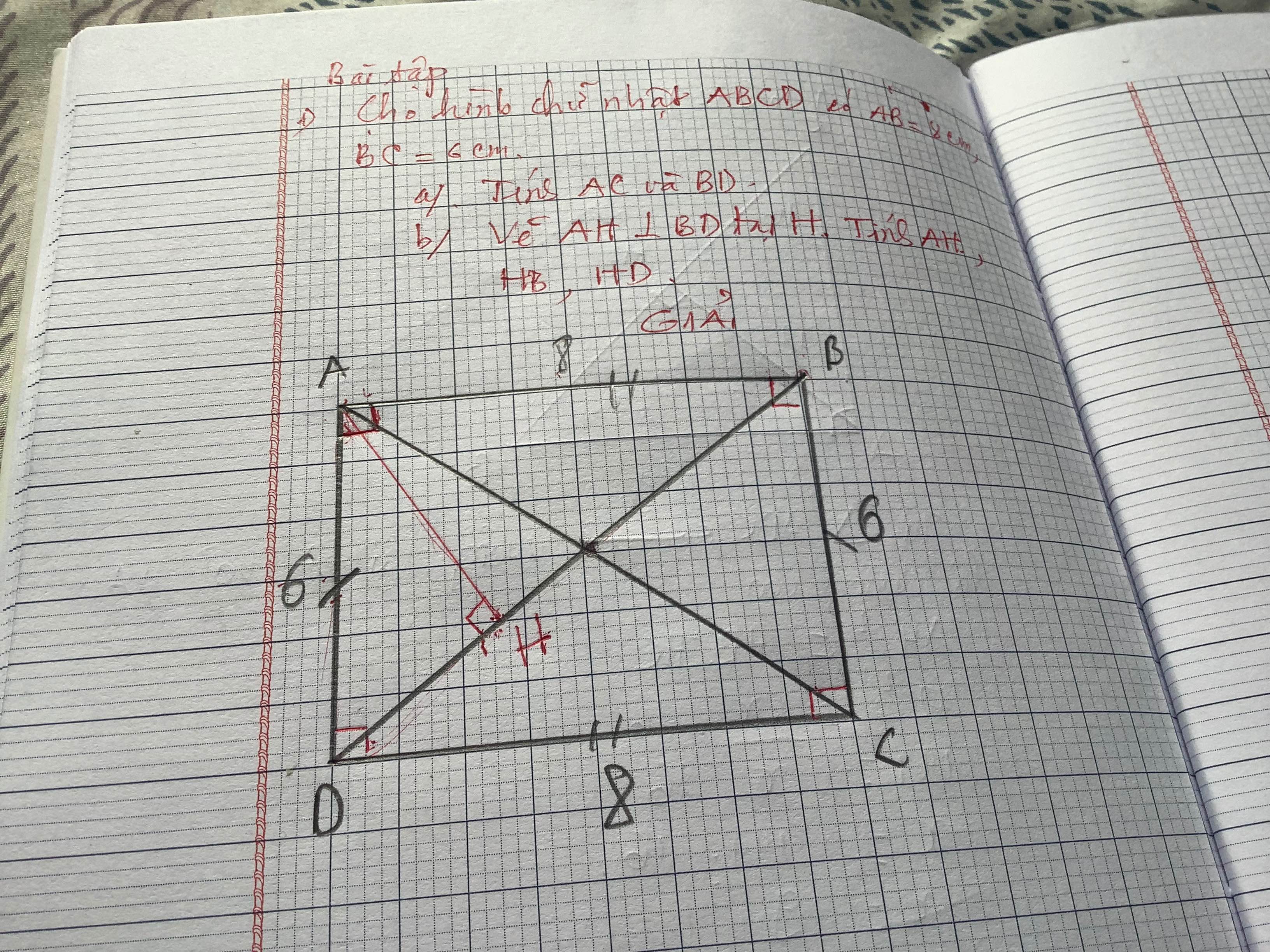
a, Áp dụng định lý Py-ta-go trong tam giác vuông ABC ta có:
\(AB^2+BC^2=AC^2\) \(\Leftrightarrow AC^2=8^2+6^2=100\) \(\Rightarrow AC=10\) cm (vì AC > 0)
b, Áp dụng hệ thức lượng trong tam giác vuông ABD ta có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AD^2}\) \(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{1}{8^2}+\dfrac{1}{6^2}=\dfrac{25}{576}\)\(\Leftrightarrow AH^2=\dfrac{576}{25}\)
\(\Rightarrow AH=\dfrac{24}{5}=4,8\) cm (vì AH > 0)
Áp dụng định lý Py-ta-go trong tam giác vuông ABH ta có:
\(AB^2=AH^2+BH^2\) \(\Leftrightarrow BH^2=AB^2-AH^2=8^2-4,8^2=40,96\)
\(\Rightarrow BH=6,4\) cm (vì BH > 0)
Vì ABCD là hình chữ nhật \(\Rightarrow AC=BD\)
\(\Leftrightarrow DH+BH=AC=10\)\(\Leftrightarrow DH=10-BH=10-6,4=3,6cm\)
a: AC=10cm
BD=19cm
b: \(AH=\dfrac{6\cdot8}{10}=4.8\left(cm\right)\)
\(HB=\dfrac{AB^2}{AC}=\dfrac{64}{10}=6.4\left(cm\right)\)
HD=10-6,4=3,6cm

 giúp em bài đó với
giúp em bài đó với






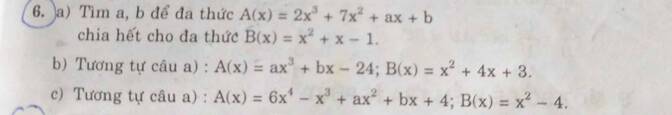

 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ

 cd
cd



