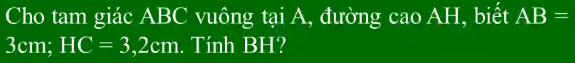Áp dụng hệ thức lượng trong tam giác vuông ABC :
\(AB^2=HB\cdot BC\)
\(\Leftrightarrow AB^2=HB\cdot\left(HB+HC\right)\)
\(\Leftrightarrow3^2=HB^2+3.2HB\)
\(\Leftrightarrow HB^2+3.2HB-9=0\)
\(\Leftrightarrow\left[{}\begin{matrix}HB=1.8\left(N\right)\\HB=-5\left(L\right)\end{matrix}\right.\)
Ta có: \(BH+HC=BC\Rightarrow BC=BH+3,2\)
Áp dụng hệ thức lượng:
\(AB^2=BH.BC\)
\(\Leftrightarrow3^2=BH.\left(BH+3,2\right)\)
\(\Leftrightarrow BH^2+3,2BH-9=0\) (bấm máy phương trình bậc 2: \(x^2+3,2x-9=0\))
\(\Rightarrow\left[{}\begin{matrix}BH=-5< 0\left(loại\right)\\BH=1,8\end{matrix}\right.\)
Vậy \(BH=1,8\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH
\(\Rightarrow AB^2=BH.BC=BH\left(BH+CH\right)\Rightarrow3^2=BH\left(BH+3,2\right)\)
\(\Rightarrow BH^2+3,2BH=9\Rightarrow BH^2+\dfrac{16}{5}BH-9=0\)
\(\Rightarrow5BH^2+16BH-45=0\Rightarrow\left(BH+5\right)\left(5BH-9\right)=0\)
mà \(BH>0\Rightarrow BH=\dfrac{9}{5}\) (cm)