a) Thu gọn và sắp xếp:
\(M\left(x\right)=6x^3+2x^4-x^2+3x^2-2x^3-x^4+1-4x^3\)
\(=\left(2x^4-x^4\right)+\left(6x^3-2x^3-4x^3\right)+\left(-x^2+3x^2\right)+1\)
\(=x^4+2x^2+1\)
b) \(M\left(x\right)+N\left(x\right)\)
\(=\left(x^4+2x^2+1\right)+\left(-5x^4+x^3+3x^2-3\right)\)
\(=x^4+2x^2+1-5x^4+x^3+3x^2-3\)
\(=-4x^4+x^3+5x^2-2\)
c) \(P\left(x\right)+N\left(x\right)=M\left(x\right)\)
\(\Rightarrow P\left(x\right)=M\left(x\right)-N\left(x\right)\)
\(\Rightarrow P\left(x\right)=\left(x^4+2x^2+1\right)-\left(-5x^4+x^3+3x^2-3\right)\)
\(\Rightarrow P\left(x\right)=x^4+2x^2+1+5x^4-x^3-3x^2+3\)
\(\Rightarrow P\left(x\right)=6x^4-x^3-x^2+4\)
d) \(M\left(x\right)=x^4+2x^2+1=x^4+x^2+x^2+1=x^2\left(x^2+1\right)+\left(x^2+1\right)=\left(x^2+1\right)^2\)
Mà: \(x^2+1\ge1\forall x\Rightarrow\left(x^2+1\right)^2\ge1>0\forall x\)
⇒ Đa thức M(x) không có nghiệm

 Ai đó giúp mik câu d) vs
Ai đó giúp mik câu d) vs



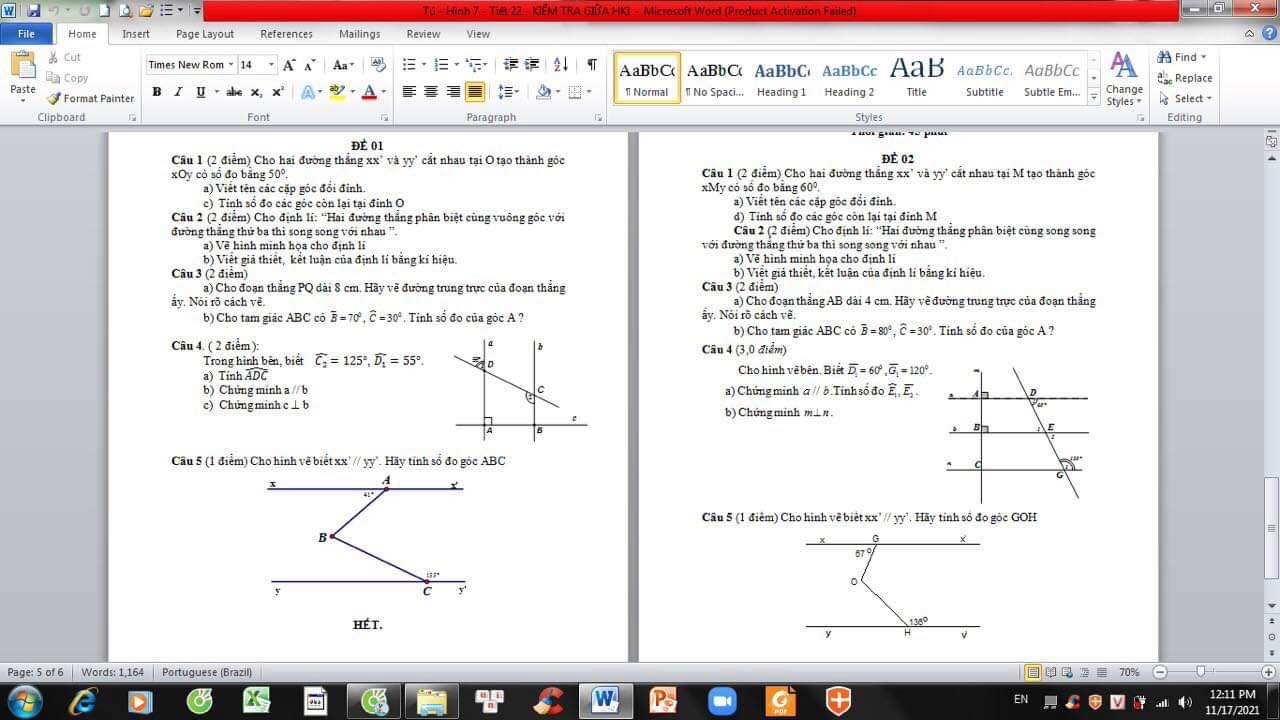



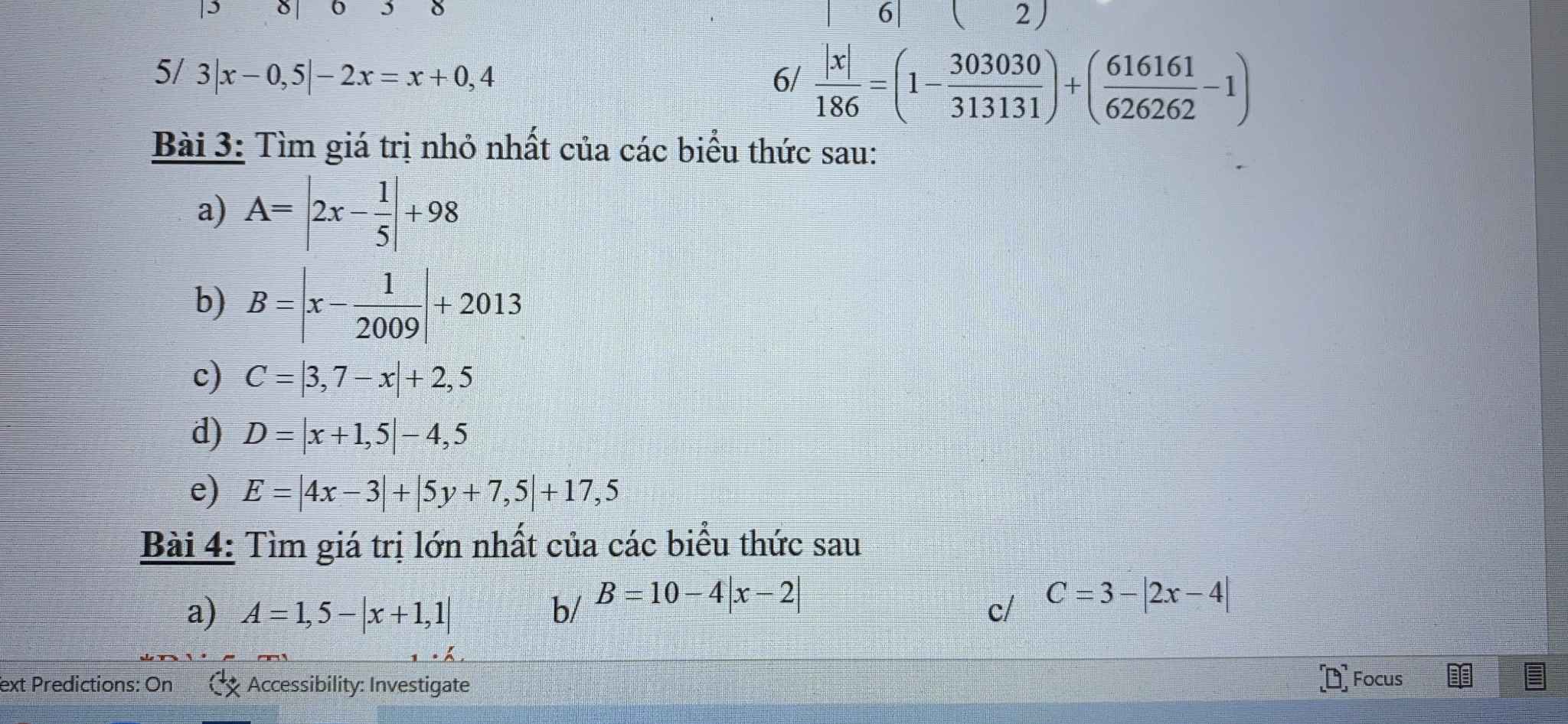











 giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước
giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước