\(a,A=\dfrac{2+6}{6}=\dfrac{8}{6}=\dfrac{4}{3}\\ b,B=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ B=\dfrac{\sqrt{x}}{\sqrt{x}-2}\\ c,P=\dfrac{A}{B}=\dfrac{2+\sqrt{x}}{\sqrt{x}}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}}=\dfrac{x-4}{x}\\ Px\le\dfrac{3}{2}\left(\sqrt{x}-1\right)\Leftrightarrow x-4\le\dfrac{3}{2}\left(\sqrt{x}-1\right)\\ \Leftrightarrow2x-8\le3\sqrt{x}-3\\ \Leftrightarrow2x-3\sqrt{x}-5\le0\\ \Leftrightarrow\left(2\sqrt{x}-5\right)\left(\sqrt{x}+1\right)\le0\\ \Leftrightarrow-1\le\sqrt{x}\le\dfrac{5}{2}\Leftrightarrow1\le x\le\dfrac{25}{4};x\ne4\)
Đúng 3
Bình luận (0)
Các câu hỏi tương tự
phần giai thừa lớp 11 các anh chị hoặc bạn có thế giải thích cho em phần này đc ko? nếu như (x-2)! thì phân tích như nào với (2-x)! thì phân tích như nào với (x+2)! với (2+x)! thì nó có khác nhau ko ạ
5x²+14x-432
Cho em hỏi là mình phân tích thành nhân tử như thế nào vậy ạ, tại số này lớn quá em ko biết tách ạ, anh nào có thể chỉ e cách tách số lớn như vậy đc ko ạ
câu này làm như thế nào ạ ?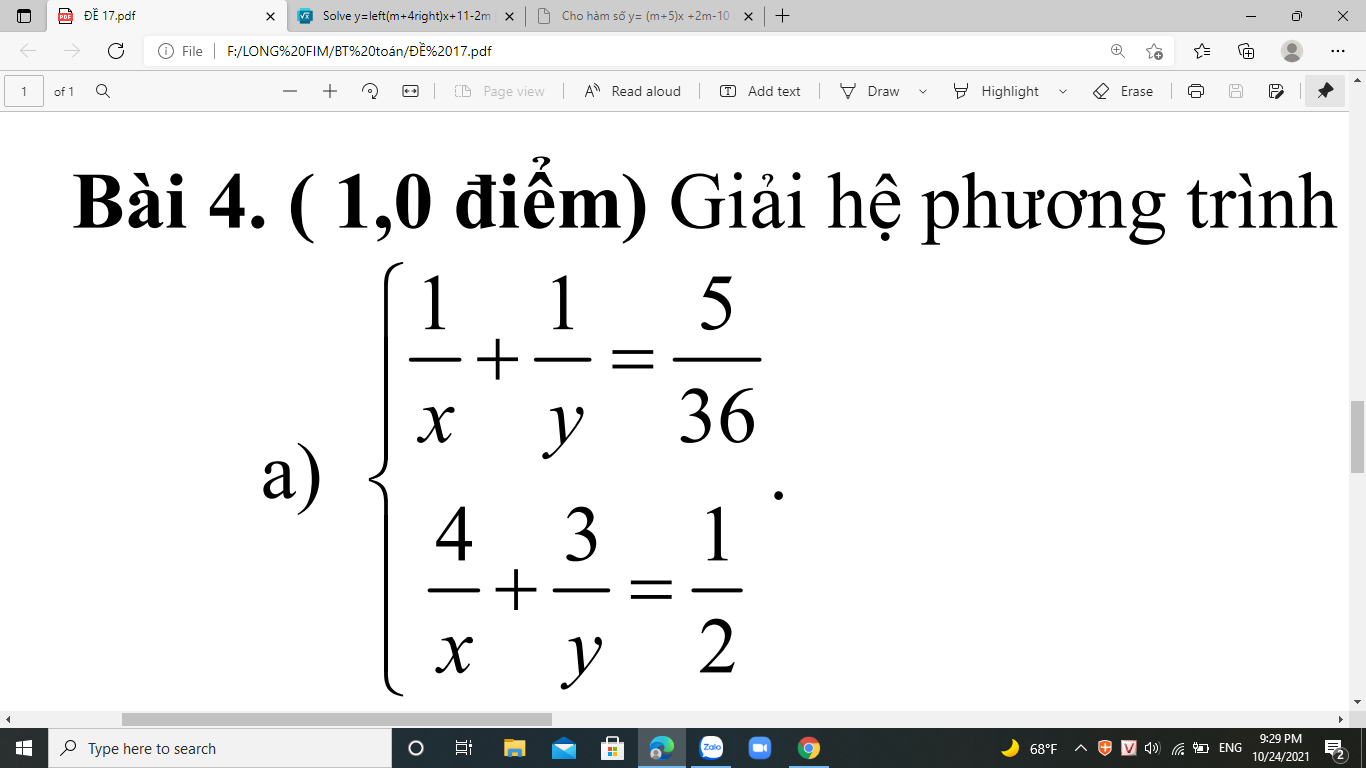
Mọi người ơi làm sao để tính \(\sin x=\dfrac{27}{32}\) trên máy tính CASIO fx-570ES PLUS ạ =((? Trong sgk chỉ ghi mỗi dòng CASIO fx-220 từ lâu rồi nên em cũng biết làm như thế nào ạ =((
Câu c làm thế nào ạ 
Đề: Cho 3 số thực dương a, b, c thỏa . Tìm GTNN Cho mình hỏi với một số bài không đối xứng như trên thì làm thế nào để đoán được dấu xảy ra ở đâu vậy ạ?
Đọc tiếp
Đề: Cho 3 số thực dương a, b, c thỏa  . Tìm GTNN
. Tìm GTNN 
Cho mình hỏi với một số bài không đối xứng như trên thì làm thế nào để đoán được dấu "=" xảy ra ở đâu vậy ạ?
cho mình hỏi làm thế nào để biết dc khi nào thì t nên dùng sin, cos , tan , cot để tính cạnh và tỉ số lượng giác trong tam giác vuông vậy . mình chưa biết phải làm như thế nào
100 đồng xu đặt lẫn lộn mặt xấp và ngửa trên bàn. Có 10 đồng xấp và 90 đồng ngửa. Bạn không hề biết được đồng nào xấp hay ngửa, không được sờ vào đồng xu, không được nhìn.
Làm thế nào để chia 100 đồng xu đó thành 2 phần mà phần nào cũng có số lượng mặt xấp như nhau.
100 đồng xu đặt lẫn lộn mặt xấp và ngửa trên bàn. Có 10 đồng xấp và 90 đồng ngửa. Bạn không hề biết được đồng nào xấp hay ngửa, không được sờ vào đồng xu, không được nhìn.
Làm thế nào để chia 100 đồng xu đó thành 2 phần mà phần nào cũng có số lượng mặt xấp như nhau.

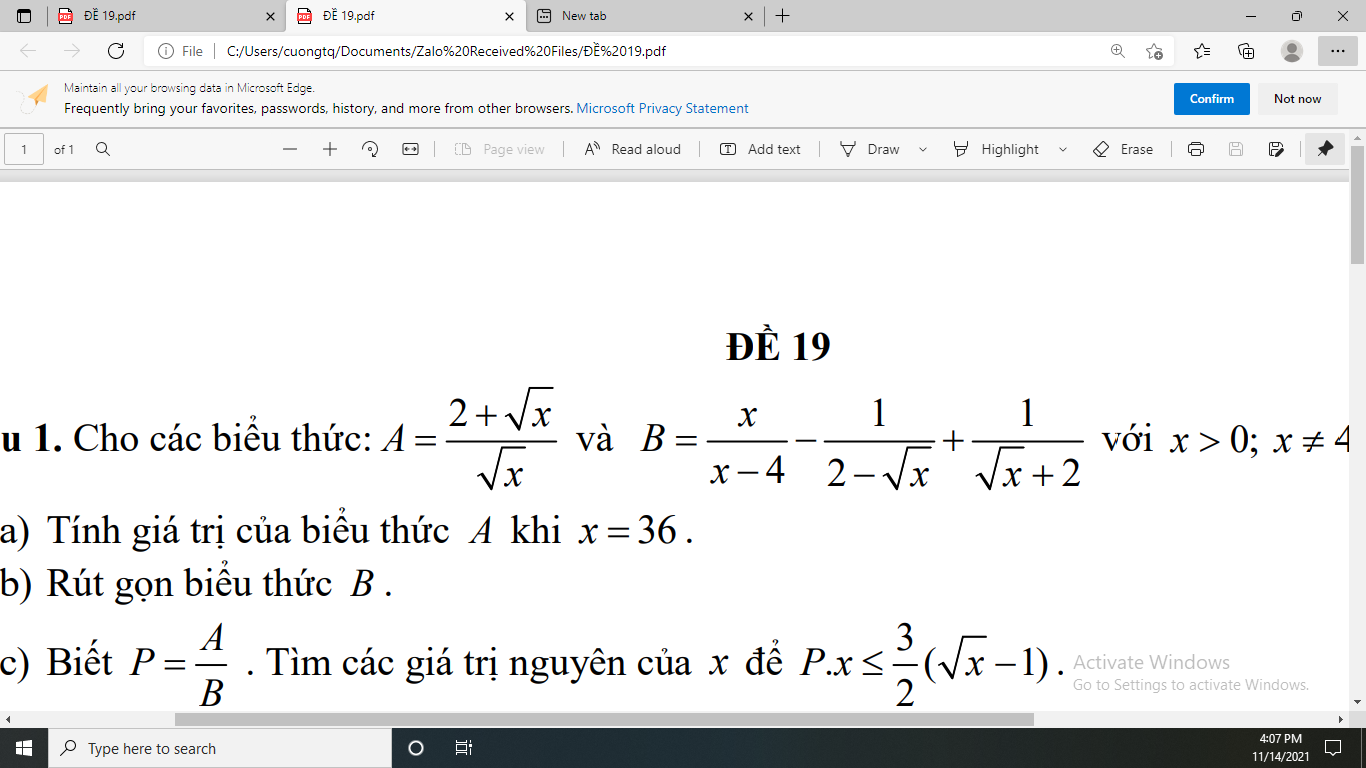 ai biết phần c làm như thế nào ko ạ
ai biết phần c làm như thế nào ko ạ










