a) \(Q=\dfrac{\left(x+2\right)^2}{x}\cdot\left(1-\dfrac{x^2}{x+2}\right)-\dfrac{x^2+10x+4}{x}\left(x\ne0;x\ne-2\right)\)
\(Q=\dfrac{\left(x+2\right)^2}{x}\cdot\dfrac{\left(x+2\right)-x^2}{x+2}-\dfrac{x^2+10x+4}{x}\)
\(Q=\dfrac{\left(x+2\right)^2}{x}\cdot\dfrac{-x^2+x+2}{x+2}-\dfrac{x^2+10x+4}{x}\)
\(Q=\dfrac{\left(x+2\right)\left(-x^2+x+2\right)}{x}-\dfrac{x^2+10x+4}{x}\)
\(Q=\dfrac{-x^3+x^2+2x-2x^2+2x+4-x^2-10x-4}{x}\)
\(Q=\dfrac{-x^3-2x^2-6x}{x}\)
\(Q=\dfrac{x\left(-x^2-2x-6\right)}{x}\)
\(Q=-x^2-2x-6\)
b) Ta có:
\(Q=-x^2-2x-6\)
\(Q=-\left(x^2+2x+6\right)\)
\(Q=-\left[\left(x^2+2x+1\right)+5\right]\)
\(Q=-\left(x+1\right)^2-5\)
Mà: \(-\left(x+1\right)^2\le0\forall x\)
\(\Rightarrow Q=-\left(x+1\right)^2-5\le-5\forall x\)
Dấu "=" xảy ra khi:
\(x+1=0\Rightarrow x=-1\)
Vậy: \(Q_{max}=-5\Leftrightarrow x=-1\)
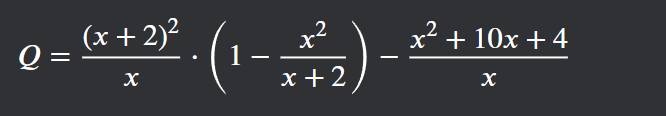
Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều
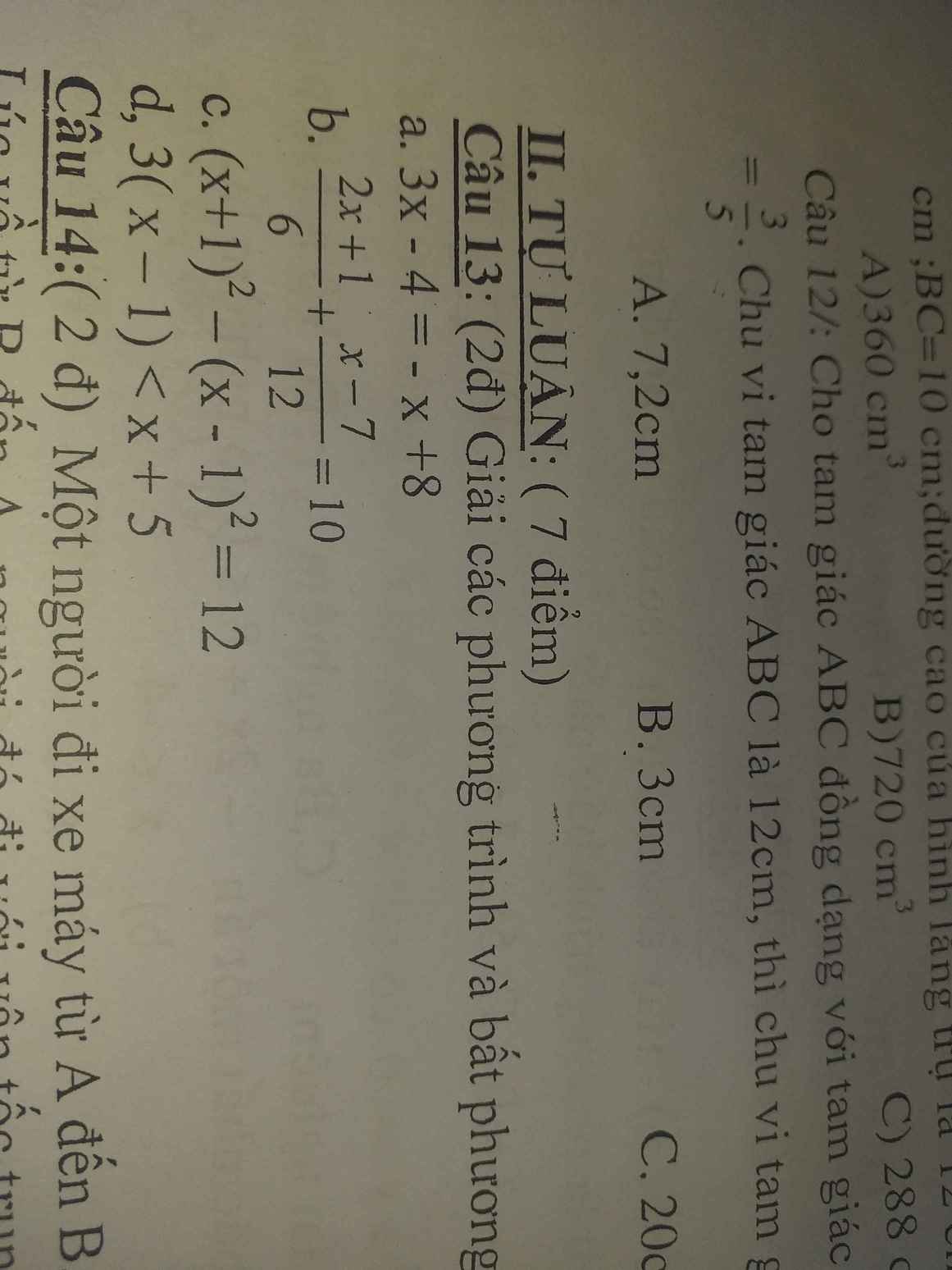
Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ
