Các câu hỏi tương tự
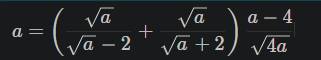với a ≥ 0, a ≠ 4
a) rút gọn biểu thức A
b) tìm giá trị của a để A - 2 < 0
c) tìm giá trị của a nguyên để biểu thức \(\dfrac{4}{A+1}\) nguyên
Cho biểu thức với . a) Rút gọn biểu thức ; b) Tìm điều kiện của để ; c) Tìm các giá trị nguyên của để có giá trị nguyên; d)* Với , hãy tìm giá trị lớn nhất của . Bài 8: Cho biểu thức ; với . a) Tính giá trị biểu thức khi . b) Rút gọn biểu thức . c) So sánh với 1. d) Tìm để có giá trị nguyên.
Bài 1. (2,0 điểm) Cho biểu thức: và với a) Tính giá trị biểu thức B khi x 9.b) Rút gọn Ac) Chứng minh rằng khi A 0 thì
Đọc tiếp
Bài 1. (2,0 điểm) Cho biểu thức:
và
với
a) Tính giá trị biểu thức B khi x = 9.
b) Rút gọn A
c) Chứng minh rằng khi A > 0 thì
rút gọn biểu thức a
A= \(\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
a/ rút gọn A
b/ tìm giá trị để A dương
Cho biểu thức \(A=x-\left(\frac{1}{\sqrt{x}-\sqrt{x-1}}-\frac{1}{\sqrt{x}+\sqrt{x-1}}\right)\)với \(x\ge1\). Rút gọn A và chứng tỏ rằng giá trị của biểu thức A luôn không âm
Cho biểu thức
A =\(\left(\dfrac{\sqrt{a}}{\sqrt{a}-2}+\dfrac{\sqrt{a}}{\sqrt{a}-2}\right).\dfrac{a-4}{\sqrt{4a}}\) với a ≥0,a≠4
a) Rút gọn biểu thức A
b) Tìm giá trị của a để A -2 < 0
c) Tìm giá trị của a nguyên để biểu thức \(\dfrac{4}{A+1}\)
Cho biểu thức M= \(\dfrac{a}{\sqrt{ab}+b}+\dfrac{b}{\sqrt{ab}-a}-\dfrac{a+b}{\sqrt{ab}}\)nhau.với hai số a, b dương khác
a/ Rút gọn M
b/Tính giá trị của M khi a=\(\sqrt{6+2\sqrt{5}}\),b=\(\sqrt{6-2\sqrt{5}}\)
Cho biểu thức Với 1) Rút gọn biểu thức 2) Tìm các giá trị của a để nhận giá trị nguyên.
Đọc tiếp
Cho biểu thức 
Với 
1) Rút gọn biểu thức 
2) Tìm các giá trị của a để nhận giá trị nguyên.
a√a−1a−√a−a√a+1a+√a+(√a−1√a).(3√a√a−1−2+√a√a+1)��−1�−�−��+1�+�+(�−1�).(3��−1−2+��+1)a) Tìm ĐKXĐ và rút gọn P√a+7�+7c) CMR: Với mọi giá trị thích hợp của a thì P 6
Đọc tiếp
a) Tìm ĐKXĐ và rút gọn P
c) CMR: Với mọi giá trị thích hợp của a thì P > 6