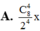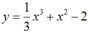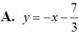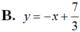a. cho cấp số cộng Un biết U5=18 và 4Sn=S2n tìm số hạn đầu u1 và công sai d của cấp số cộng
b. cho ba số a,b,c là ba số liên tiếp của một cấp số cộng có công sai là 2. Nếu tăng số thứ nhất thêm 1, tăng số thứ 2 thêm 1 và số thứ ba thêm 3 thì được ba số mới là ba số liên tiếp của một cấp số nhân. Tính a+b+c
a.
\(u_5=18\Rightarrow u_1+4d=18\) (1)
\(4S_n=S_{2n}\Rightarrow\dfrac{4n\left(2u_1+\left(n-1\right)d\right)}{2}=\dfrac{2n\left(2u_1+\left(2n-1\right)d\right)}{2}\)
\(\Rightarrow4u_1+2\left(n-1\right)d=2u_1+\left(2n-1\right)d\)
\(\Rightarrow2u_1-d=0\Rightarrow d=2u_1\) (2)
Thế (2) vào (1):
\(\Rightarrow9u_1=18\Rightarrow u_1=2\Rightarrow d=4\)
b.
Do a;b;c là 3 số hạng liên tiếp của 1 CSC công sai 2 nên: \(\left\{{}\begin{matrix}b=a+2\\c=a+4\end{matrix}\right.\)
Khi tăng số thứ nhất thêm 1, số thứ 2 thêm 1 và số thứ 3 thêm 3 được 1 cấp số nhân nên:
\(\left(a+1\right)\left(c+3\right)=\left(b+1\right)^2\)
\(\Rightarrow\left(a+1\right)\left(a+7\right)=\left(a+3\right)^2\)
\(\Rightarrow a^2+8a+7=a^2+6a+9\)
\(\Rightarrow a=1\Rightarrow b=3\Rightarrow c=5\)