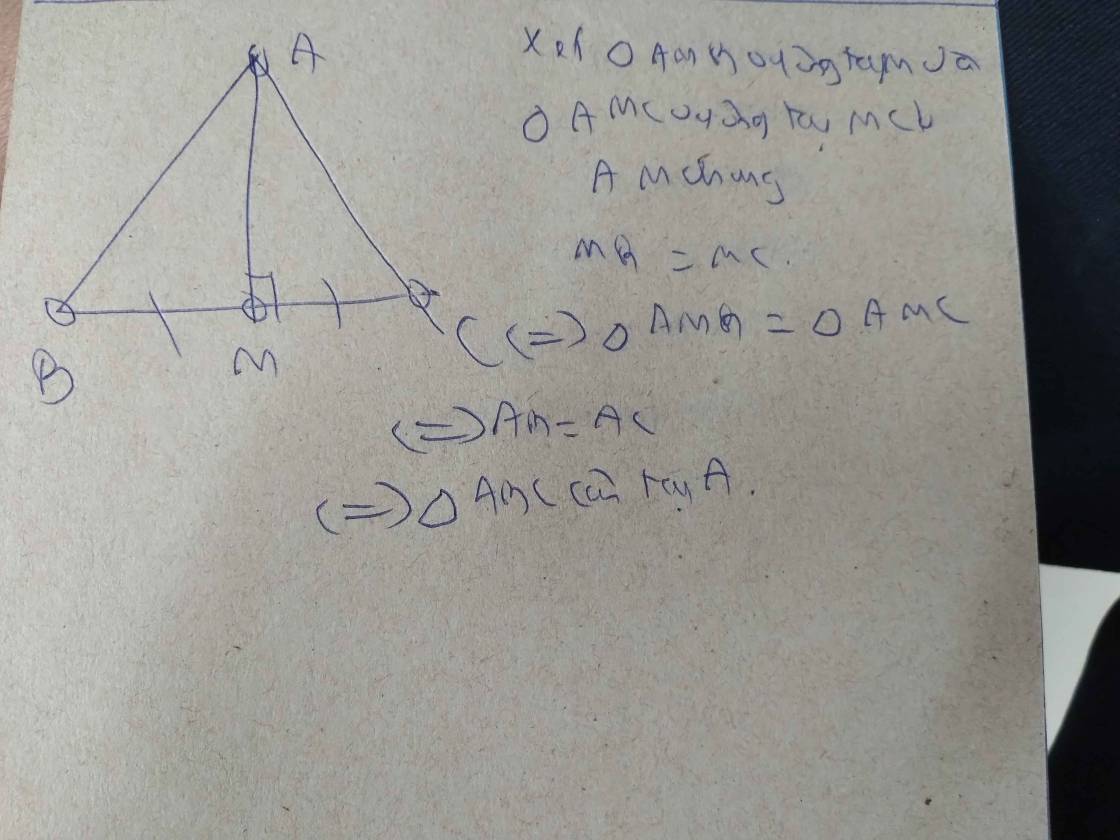Các câu hỏi tương tự
Nhận xét Trong một tam giác, nếu hai trong bốn loại đường ( đường trung tuyến, đường phân giác, đường cao cùng xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của cạnh này ) trùng nhau thì tam giác đó là một tam giác cân.Từ nhận xét trên hãy chứng minh: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân ai nhank mk tick cho help me tói 9h tối nay phải có nha mk gấp lắm
Đọc tiếp
Nhận xét
Trong một tam giác, nếu hai trong bốn loại đường ( đường trung tuyến, đường phân giác, đường cao cùng xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của cạnh này ) trùng nhau thì tam giác đó là một tam giác cân.
Từ nhận xét trên hãy chứng minh: "Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân "
ai nhank mk tick cho help me tói 9h tối nay phải có nha mk gấp lắm
bài 1: chứng minh 1 tam có 2 đường trung tuyến bằng nhau thì tam giác đó cân
bài 2: chứng minh trong tam giác cân 2 đường cao ứng với 2 cạnh bên và ngược lại có 2 đường cao bằng nhau là tam giác cân
bài 3:chứng minh 2 đường phân giác xuất phát từ 2 đỉnh ở đấy của tam giác cân thì bằng nhau và ngược lại 1 tam giác có 2 đg phân giác bằng nhau thì là tam giác ân
chứng minh rằng trong một tam giác đường cao không lớn hơn đường trung tuyến xuất phát từ cùng một đỉnh
Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
mạng mạng
Chứng minh rằng trong một tam giác, đường cao không lớn hơn đường trung tuyến xuất phát từ một đỉnh.
1.1. Vẽ đường trung tuyến, đường phân giác, đường trung trực, đường cao cùng
xuất phát từ một đỉnh của một tam giác bất kì.
1.2. Vẽ đường trung tuyến, đường phân giác, đường trung trực, đường cao cùng
xuất phát từ một đỉnh của một tam giác cân.
chứng minh rằng trong một tam giác cân đường cao suất phát từ định đối diện với cạnh đáy đồng thời là đường phân giác cùng xuất phát từ đỉnh này
Chứng minh rằng: Nếu 1 tam giác có đường cao và đường trung tuyến ứng với 1 cạnh (xuất phát từ 1 đỉnh) chia góc ở đỉnh đó thành 3 phần bằng nhau thì tam giác ấy vuông
Chứng minh một tam giác có 2 đường cao (xuất phát từ các đỉnh của 2 góc nhọn) bằng nhau thì tam giác đó là tam giác cân.Từ đó suy ra một tam giác có 3 đường cao bằng nhau thì tam giác đó là tam giác đều.