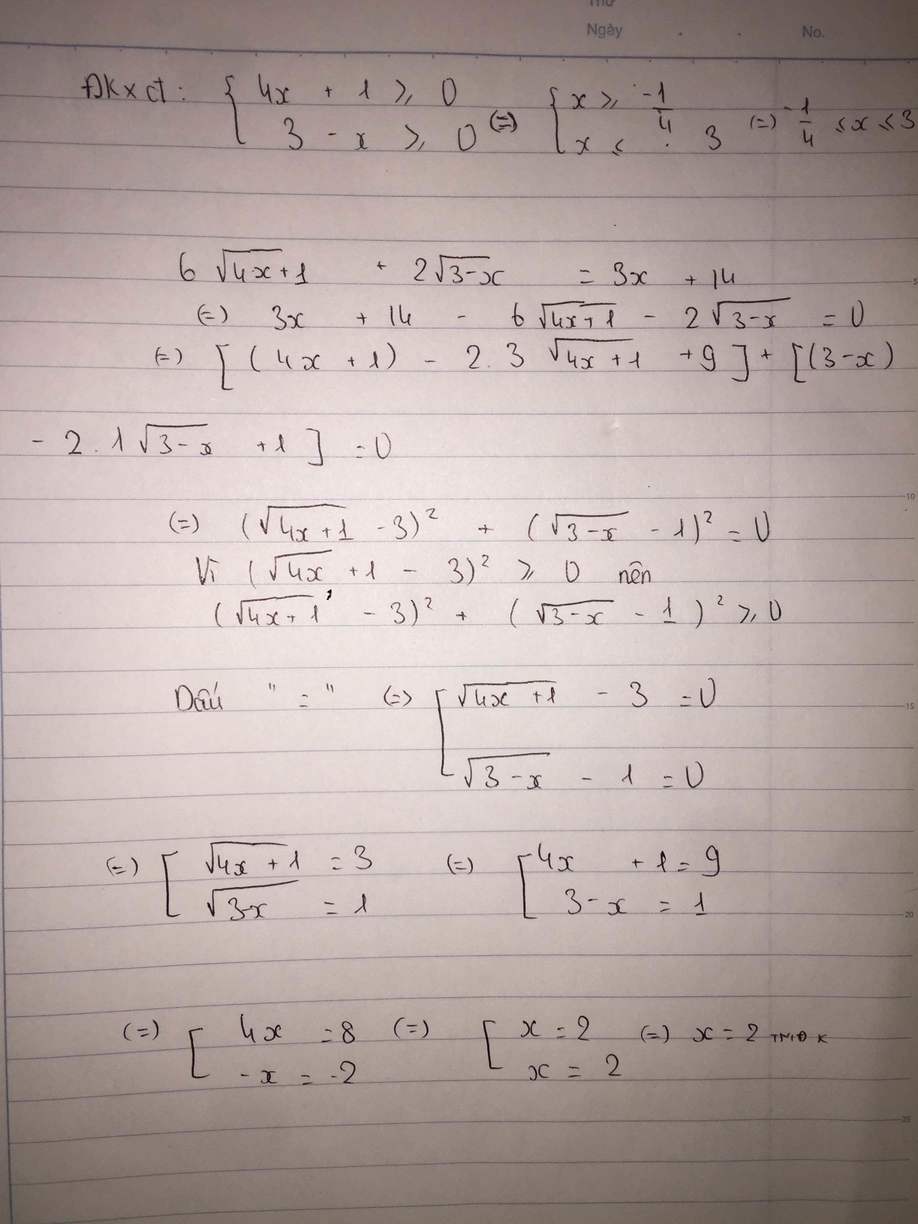Các câu hỏi tương tự
Phương pháp 6. Biến đổi về dạng \(A^2=B^2\)
a \(x^2+4\sqrt{x+3}=3x+6\)
b \(4x^2+14x+11=4\sqrt{6x+10}\)
c \(4\sqrt{x+1}=x^2-5x+14\)
giai pt sau
\(\sqrt{3x-1}-\sqrt{x+2}.\sqrt{3x^2+7x+2}+4=4x-2\)
\(x^2-5x+3.\sqrt{2x-1}=2.\sqrt{14-2x}+5\)
\(\left(x+1\right)\left(x+4\right)-3\sqrt{x^2+5x+2}=6\)
Câu 2: Tìm x biết:
a. \(\sqrt{x-1}=2\)
b. \(\sqrt{3x+1}=\sqrt{4x-3}\)
c. \(\sqrt{4x+20}-3\sqrt{5+x}+\dfrac{4}{3}\sqrt{9x+45}=6\)
d. \(\sqrt{x^2-4x+4}=\sqrt{6+2\sqrt{5}}\)
Giải phương trình:
\(6\sqrt{4x+1}+2\sqrt{3-x}=3x+14\)
\(6\sqrt{4x+1}+2\sqrt{3-x}=3x+14\)
giải pt trên
Giair phương trình :
a,\(4x-15\sqrt{x}+14=0\)
b,\(\sqrt{x+1}+1=4x^2+\sqrt{3x}\)
giải phương trình sau:
a) \(4x^2+\left(8x-4\right).\sqrt{x}-1=3x+2\sqrt{2x^2+5x-3}\)
b) \(8x^3-36x^2+\left(1-3x\right)\sqrt{3x-2}-3\sqrt{3x-2}+63x-32=0\)
c) \(2\sqrt[3]{3x-2}-3\sqrt{6-5x}+16=0\)
d) \(\sqrt[3]{x+6}-2\sqrt{x-1}=4-x^2\)
Giải các phương trình sau a , 2+sqrt{x+2}x.sqrt{x+2} b, x^2+3x+1left(x+3right).sqrt{x^2+1} c, sqrt{4x^2+8x+29}+sqrt{2y^2+12y+19}6 d, sqrt{5x^2+10x+14}+sqrt{3x^2+6x+7}-x^2-2x+4 e, sqrt{4x+7}+xsqrt{2x+1}-3f,sqrt{4x^2+5x+1}-9x2sqrt{x^2-x+1}-3
Đọc tiếp
Giải các phương trình sau
a , \(2+\sqrt{x+2}=x.\sqrt{x+2}\)
b, \(x^2+3x+1=\left(x+3\right).\sqrt{x^2+1}\)
c, \(\sqrt{4x^2+8x+29}+\sqrt{2y^2+12y+19}=6\)
d, \(\sqrt{5x^2+10x+14}+\sqrt{3x^2+6x+7}=-x^2-2x+4\)
e, \(\sqrt{4x+7}+x=\sqrt{2x+1}-3\)
f,\(\sqrt{4x^2+5x+1}-9x=2\sqrt{x^2-x+1}-3\)
1) x+1+sqrt{x^2-4x+1}3sqrt{x}2) 4x^3+x-left(x+1right)sqrt{2x+1}03) x-sqrt{x}1-sqrt{2left(x^2-x+1right)}4) sqrt{x+1}+sqrt{4-x}+sqrt{left(x+1right)left(4-xright)}55) sqrt{3x-2}+sqrt{x-1}4x-9+2sqrt{3x^2-5x+2}6) 3sqrt{x+2}-6sqrt{2-x}+4sqrt{4-x^2}10-3x
Đọc tiếp
1) \(x+1+\sqrt{x^2-4x+1}=3\sqrt{x}\)
2) \(4x^3+x-\left(x+1\right)\sqrt{2x+1}=0\)
3) \(x-\sqrt{x}=1-\sqrt{2\left(x^2-x+1\right)}\)
4) \(\sqrt{x+1}+\sqrt{4-x}+\sqrt{\left(x+1\right)\left(4-x\right)}=5\)
5) \(\sqrt{3x-2}+\sqrt{x-1}=4x-9+2\sqrt{3x^2-5x+2}\)
6) \(3\sqrt{x+2}-6\sqrt{2-x}+4\sqrt{4-x^2}=10-3x\)