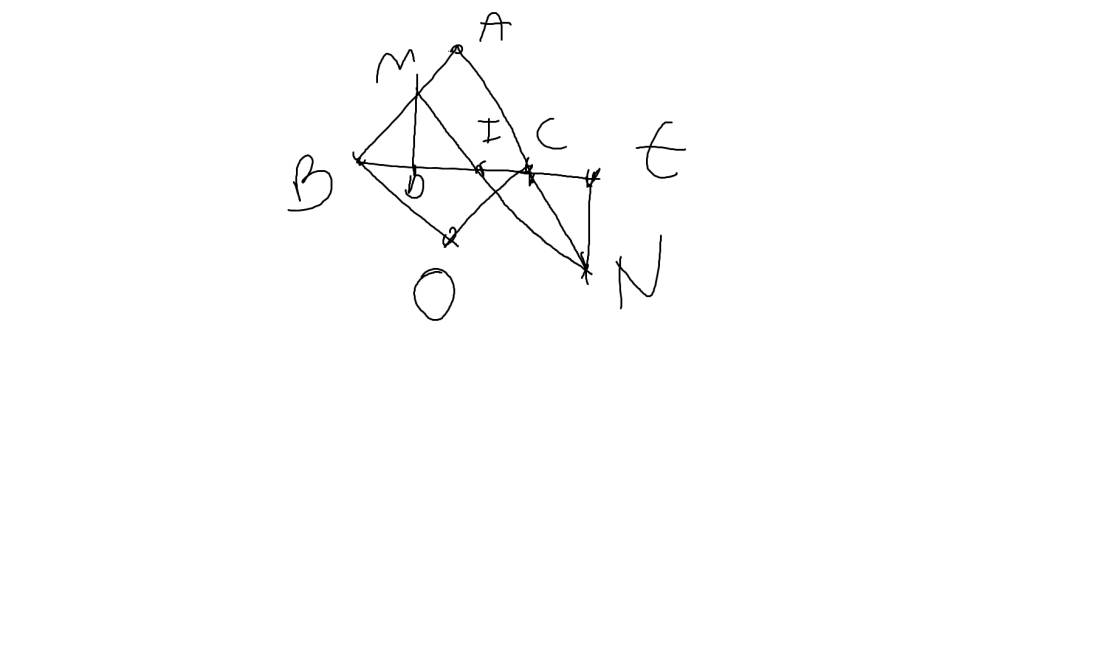
2) Cho ΔABC cân tại A . Trên tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Từ D kẻ đường vuông góc với BC cắt AB ở M. Từ E kẻ đường vuông góc với BC cắt AC ở N.
a) Chứng minh MD = NE.
b) Biết MN cắt DE tại I. Chứng minh I là trung điểm DE.
c) Đường thẳng kẻ từ C vuông góc với AC cắt đường thẳng kẻ từ B vuông góc với AB tại O. CM: AO là trung trực của BC
vẽ cả hình giúp em ạ em cảm ơn
a: ta có: \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
mà \(\widehat{ACB}=\widehat{NCE}\)(hai góc đối đỉnh)
nên \(\widehat{ABC}=\widehat{NCE}\)
Xét ΔMDB vuông tại D và ΔNEC vuông tại E có
DB=EC
\(\widehat{DBM}=\widehat{ECN}\)
Do đó: ΔMDB=ΔNEC
=>MD=NE
b: Ta có: MD\(\perp\)BC
NE\(\perp\)BC
Do đó: MD//NE
Xét ΔIDM vuông tại D và ΔIEN vuông tại E có
MD=NE
\(\widehat{IMD}=\widehat{INE}\)
Do đó: ΔIDM=ΔIEN
=>ID=IE
=>I là trung điểm của DE
c: Xét ΔABO vuông tại B và ΔACO vuông tại C có
AO chung
AB=AC
Do đó: ΔABO=ΔACO
=>OB=OC
=>O nằm trên đường trung trực của BC(1)
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AO là đường trung trực của BC