`y=f(x)>0AAx\in(0,2)` là sai
vì tại `x\in(0,1)` thì `f(x)<0`
`y=f(x)>0AAx\in(0,2)` là sai
vì tại `x\in(0,1)` thì `f(x)<0`
Cho hàm số f(x) nhận giá trị dương, có đạo hàm liên tục trên [0;2]. Biết f(0) =1 và f x f 2 - x = e 2 x 2 - 4 x với mọi x ∈ [ 0 ; 2 ] . Tính tích phân I = ∫ 0 2 x 3 - 3 x 2 f ' x f x dx .
A. I = -14/3
B. I = -32/5
C. I = -16/3
D. I = -16/5
Giả sử hàm số y=f(x) liên tục, nhận giá trị dương trên 0 ; + ∞ và thỏa mãn f(1)=1, f ( x ) = f ' ( x ) 3 x + 1 , với mọi x>0. Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()
Xét các khẳng định sau
i) Nếu hàm số y=f(x) có đạo hàm dương với mọi x thuộc tập số D thì f x 1 < f x 2 ∀ x 1 , x 2 ∈ D , x 1 < x 2
ii) Nếu hàm số y=f(x) có đạo hàm âm với mọi x thuộc tập số D thì f x 1 > f x 2 ∀ x 1 , x 2 ∈ D , x 1 < x 2
iii) Nếu hàm số y=f(x) có đạo hàm dương với mọi x thuộc R thì f x 1 < f x 2 ∀ x 1 , x 2 ∈ R , x 1 < x 2
iv) Nếu hàm số y=f(x) có đạo hàm âm với mọi x thuộc R thì f x 1 > f x 2 ∀ x 1 , x 2 ∈ R , x 1 < x 2
Số khẳng định đúng là
A. 1
B. 2
C. 3
D. 4
Cho hàm số f(x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;2] thoả mãn f(0) = 3; f(2) = 12 và ∫ 0 2 ( f ' ( x ) ) 2 f ( x ) d x = 6 Tính f(1)
A. 27/4
B. 25/4
C. 9/2
D. 15/4
Cho hàm số y = 2 x - m x + 2 với m là tham số , m ≠ 4 . Tìm giá trị của tham số m thỏa mãn min f ( x ) x ∈ [ 0 ; 2 ] + m a x f ( x ) x ∈ [ 0 ; 2 ] = - 8
A. m= 8
B. m= 9
C. m= -12
D. m= 10
Cho hàm số y=f(x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;3] thoả mãn f(0)=3, f(3)=8 và ∫ 0 3 ( f ' ( x ) ) 2 f ( x ) + 1 d x = 4 3 Giá trị của f(2) bằng
A. 64 9
B. 55 9
C. 16 3
D. 19 3
Cho hàm số y = f(x) liên tục trên ℝ sao cho m a x x ∈ [ 0 ; 10 ] f ( x ) = f(2) = 4. Xét hàm số g(x) = f x 3 + x - x 2 + 2 x + m . Giá trị của tham số m để m a x x ∈ [ 0 ; 2 ] g ( x ) = 8 là
A. 5
B. 4
C. -1
D. 3
Cho hàm số f(x) có đạo hàm là f'(x). Đồ thị của hàm số y = f'(x) được cho như hình vẽ dưới đây:
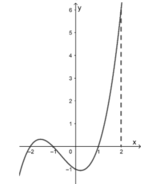
Biết rằng f(-1) + f(0) < f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f(x) trên đoạn [-1;2] lần lượt là:
A. f(1);f(2)
B. f(2);f(0)
C. f(0);f(2)
D. f(1);f(-1)
Cho hàm số y=f(x) là hàm đa thức với hệ số thực. Hình vẽ bên dưới là một phần đồ thị của hai hàm số: y=f(x) và y=f'(x)
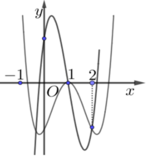
Tập các giá trị của tham số m để phương trình f ( x ) = m e x có hai nghiệm phân biệt trên [0;2] là nửa khoảng [a;b). Tổng a+b gần nhất với giá trị nào sau đây?
A. -0.81
B. -0.54
C. -0.27
D. 0.27
Cho hàm số f(x), đồ thị hàm số y=f '(x) là đường cong trong hình bên. Giá trị lớn nhất của hàm số g(x) = -f(2x-1) +2x trên đoạn [0;2] bằng