Question

Cho hàm số y = f(x) liên tục trên  ℝ  sao cho m a x x ∈ [ 0 ; 10 ] f ( x ) = f(2) = 4. Xét hàm số g(x) = f x 3 + x - x 2 + 2 x + m . Giá trị của tham số m để  m a x x ∈ [ 0 ; 2 ] g ( x )   =   8  là

A. 5

B. 4

C. -1

D. 3

Answer 1

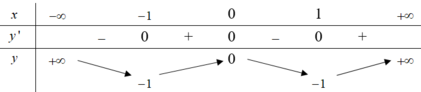
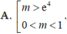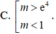Chọn D                 

Xét hàm số 

 Ta có  nên 

Vì vậy  khi t = 2  ⇔ x = 1

Mặt khác   Suy ra  khi x = 1

Vậy  ⇔ m = 3

Cách 2: Tác giả: Nguyễn Trọn  g Lễ; Fb: Nguyễn Trọng Lễ.

Phương pháp trắc nghiệm

Chọn hàm y = f(x) = 4 thỏa mãn giả thiết: hàm số y = f(x) liên tục trên  ℝ  có 

Ta có 

Xét hàm số g(x) liên tục trên đoạn [0;2], g'(x) = 0 ⇔ x = 1. Ta có g(0) = 4 + m, g(1) = 5 + m, g(2) = 4 + m

Rõ ràng g(0) = g(2) < g(1) nên 

Vậy 5 + m = 8 => m = 3