Question

1+\(\dfrac{1}{2}\)(1+2)+\(\dfrac{1}{3}\)(1+2+3)+\(\dfrac{1}{4}\)(1+2+3+4)+....+\(\dfrac{1}{20}\)(1+2+3+...+20)

=1+\(\dfrac{1}{2}\).\(\dfrac{2.3}{2}\)+\(\dfrac{1}{3}\).\(\dfrac{3.4}{2}\)+\(\dfrac{1}{4}\).\(\dfrac{4.5}{2}\)+...+\(\dfrac{1}{20}\).\(\dfrac{20.21}{2}\)

=\(\dfrac{2}{2}\)+\(\dfrac{3}{2}\)+\(\dfrac{4}{2}\)+\(\dfrac{5}{2}\)+...+\(\dfrac{21}{2}\)

=\(\dfrac{1}{2}\)(1+2+3+....+20)

=\(\dfrac{1}{2}\).\(\dfrac{20.21}{2}\)=105

mình giải như này có đúng ko mn nếu sai mn sửa lại giúp mình với. Đang gấp sắp thi rồi

Answer 1

Bạn sửa phần này nhé ! 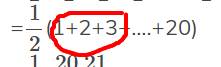 nó là 2+3+...+21 nhé sửa lại rồi thì kết quả là 115 nha không phải 105