2:
góc DBA=180-60=120 độ
góc BDA=180-120-40=20 độ
AD/sinABD=AB/sinBDA=BD/sinA
=>AD/sin120=AB/sin20=5/sin40
=>AD=6,74cm; AB=2,66cm
2:
góc DBA=180-60=120 độ
góc BDA=180-120-40=20 độ
AD/sinABD=AB/sinBDA=BD/sinA
=>AD/sin120=AB/sin20=5/sin40
=>AD=6,74cm; AB=2,66cm
Cho tứ giác ABCD với D=90 độ, A=60 độ, B=150 độ, CD=12cm. AB là cạnh hình vuông có diện tích là 108cm^2. Miền trg tứ giác có điểm M sao cho ABCM là hình bình hành. MH vuông DC
a) CM:MC là phân giác BCD
b) DMC là tam giác vuông tại M
c) Tam giác AMD cân
d) Tính AD,BC=>Tam giác ADB đều
cho tứ giác ABCD với goc D =90 do; A=60 do; B = 150 do; CD=12cm. AB là cạnh hionhf vuông có S = 108cm^2. Miền trong tứ giác có điểm M sao cho ABCM là hình bình hành. MH vuông DC
a) CM MC là phân giác BCD
b) DMC là tam giác vuông tại M
c) tam giác AMD cân
d) Tính AD,BC=> Tam giác ADB đều
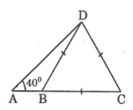
Cho hình bên. BCD là tam giác đều cạnh 5cm và góc DAB bằng 40 ° . Hãy tính: AB
1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABCgiúp với1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABCgiúp với
Cho nửa lục giác đều ABCD nội tiếp trong nửa đường tròn (O;R). Hai tiếp tuyến tại B và D cắt nhau ở T.
a) Chứng minh OT//AB
b) Chứng minh 3 điểm O, C, T thẳng hàng
c) Tính chu vi và diện tích tam giác TBD theo R
d) Tính theo R diện tích giới hạn bởi 2 cạnh TB, TD và cung BCD
giúp với
1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABCgiúp với
1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABC
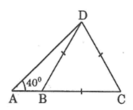
Cho hình bên. BCD là tam giác đều cạnh 5cm và góc DAB bằng 40 ° . Hãy tính: AD
Cho tam giác PQR có góc R tù, góc P bằng \(18^0\), trên cạnh PR lấy điểm T sao cho góc \(\widehat{PTQ}=150^0\), biết cạnh RT=5, TQ=8. Hãy tính
a) Độ dài cạnh PT
b) Diện tích tam giác PQR
giúp với
1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABC.
Cho tam giác ABC có góc B= 120 độ, BC= 12 cm, AB=6cm,đường phân giác góc B cắt AD tại D.
a/ Tính BD
b/ Tính tỉ số diện tích của tam giác ABD và tam giác ABC
c/ Tính diện tích tam giác ABD, tam giác BCD
d/ M là trung điểm BC. Chứng minh: AM vuông góc BD