Question

1) cho tứ diện ABCD có I ,K lần lượt là trung điểm của cạnh AD, BC. a) tìm giao tuyến của (KAD) và (BCD) b) tìm giao tuyến của (IBC) và (KAD) c) gọi MN là 2 điểm lần lượt lấy trên 2 đoạn thẳng AB và AC .tìm giao tuyến của (IBC) và (DMN)

Answer 1

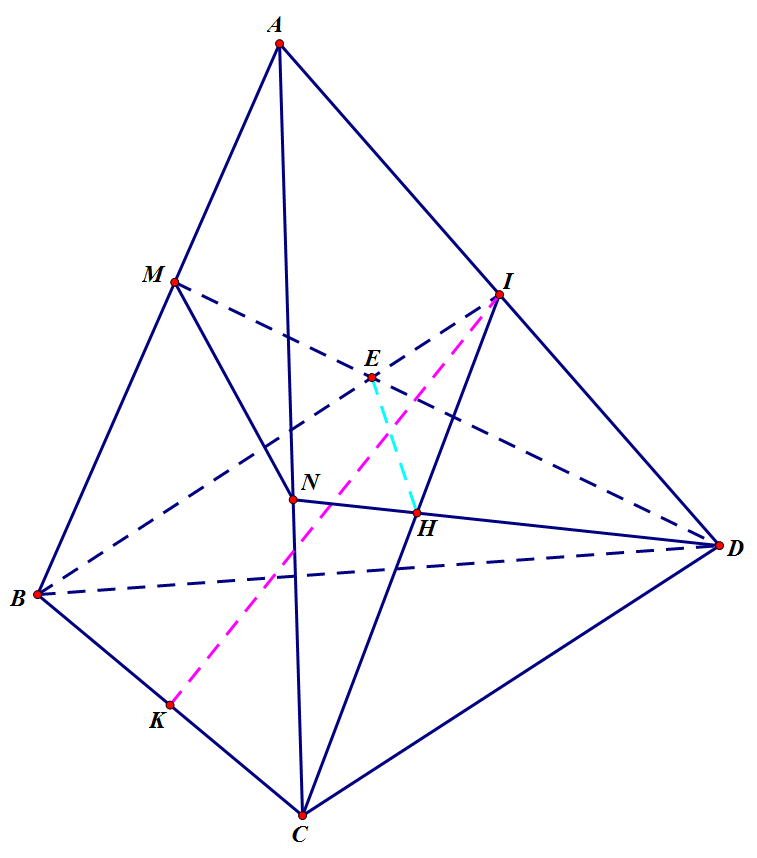
a,Hiển nhiên : K ∈ (KAD), mà K ∈ BC nên K ∈ (BCD)

Hiển nhiên : D ∈ (KAD) và D ∈ (BCD)

⇒ (KAD) \(\cap\) (BCD) = DK

b, Hiển nhiên : K ∈ (KAD), mà K ∈ BC nên K ∈ (IBC) 

Hiển nhiên I ∈ (IBC), mà I ∈ AD nên I ∈ (KAD)

⇒ (KAD) \(\cap\) (BCI) = IK

c, Trong (ABD) gọi E là giao điểm của BI và DM

⇒ \(\left\{{}\begin{matrix}E\in\left(IBC\right)\\E\in\left(DMN\right)\end{matrix}\right.\)

Trong (ACD) gọi F là giao điểm của CI và DN

⇒ \(\left\{{}\begin{matrix}F\in\left(IBC\right)\\F\in\left(DMN\right)\end{matrix}\right.\)

Vậy (DMN) \(\cap\) (IBC) = EF