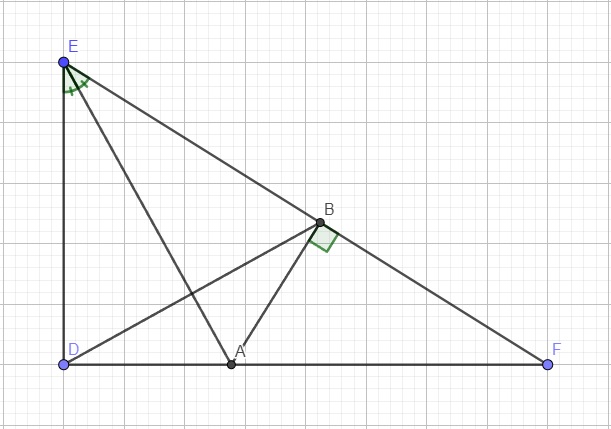
a.
Do EA là phân giác \(\Rightarrow\widehat{AED}=\widehat{AEB}\)
Xét hai tam giác vuông EDA và EBA có:
\(\left\{{}\begin{matrix}EA\text{ chung}\\\widehat{AED}=\widehat{AEB}\end{matrix}\right.\)
\(\Rightarrow\Delta_{\perp}EDA=\Delta_{\perp}EBA\left(ch-gn\right)\)
b.
Từ câu a, do \(\Delta_{\perp}EDA=\Delta_{\perp}EBA\Rightarrow\left\{{}\begin{matrix}ED=EB\\AD=AB\end{matrix}\right.\)
\(\Rightarrow EA\) là trung trực của DB
c.
Do EA là phân giác, áp dụng định lý phân giác trong tam giác ABC:
\(\dfrac{DA}{AF}=\dfrac{DE}{FE}\)
Mà tam giác DEF vuông tại D \(\Rightarrow DE< FE\) (cạnh góc vuông luôn nhỏ hơn cạnh huyền)
\(\Rightarrow\dfrac{DE}{FE}< 1\)
\(\Rightarrow\dfrac{DA}{AF}< 1\Rightarrow DA< AF\)