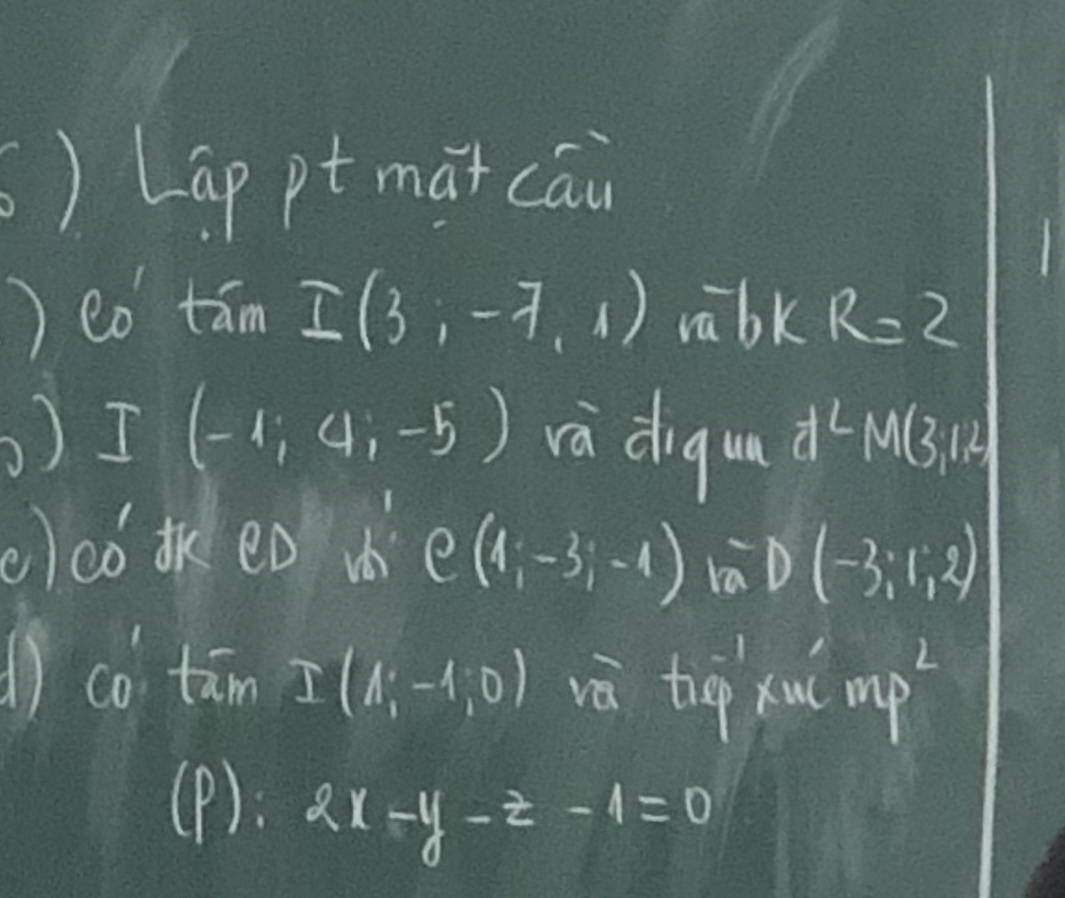a.
Phương trình:
\(\left(x-3\right)^2+\left(y+7\right)^2+\left(z-1\right)^2=4\)
b.
\(\overrightarrow{IM}=\left(4,-3,7\right)\Rightarrow R=IM=\sqrt{4^2+\left(-3\right)^2+7^2}=\sqrt{74}\)
Phương trình:
\(\left(x+1\right)^2+\left(y-4\right)^2+\left(z+5\right)^2=74\)
c.
Gọi I là trung điểm CD \(\Rightarrow I\left(-1,-1,\dfrac{1}{2}\right)\)
\(\overrightarrow{CD}=\left(-4,4,3\right)\Rightarrow R=\dfrac{1}{2}CD=\dfrac{1}{2}\sqrt{\left(-4\right)^2+4^2+3^2}=\sqrt{\dfrac{41}{4}}\)
Mặt cầu đường kính CD nhận I là tâm và bán kính R
Phương trình:
\(\left(x+1\right)^2+\left(y+1\right)^2+\left(z-\dfrac{1}{2}\right)^2=\dfrac{41}{4}\)
d.
\(d\left(I,\left(P\right)\right)=\dfrac{\left|2.1-\left(-1\right)-0-1\right|}{\sqrt{2^2+\left(-1\right)^2+\left(-1\right)^2}}=\dfrac{\sqrt{6}}{3}\)
Do mặt cầu tiếp xúc (P) nên có bán kính \(R=d\left(I,\left(P\right)\right)=\dfrac{\sqrt{6}}{3}\)
Phương trình
\(\left(x-1\right)^2+\left(y+1\right)^2+z^2=\dfrac{2}{3}\)