Question

Answer 1

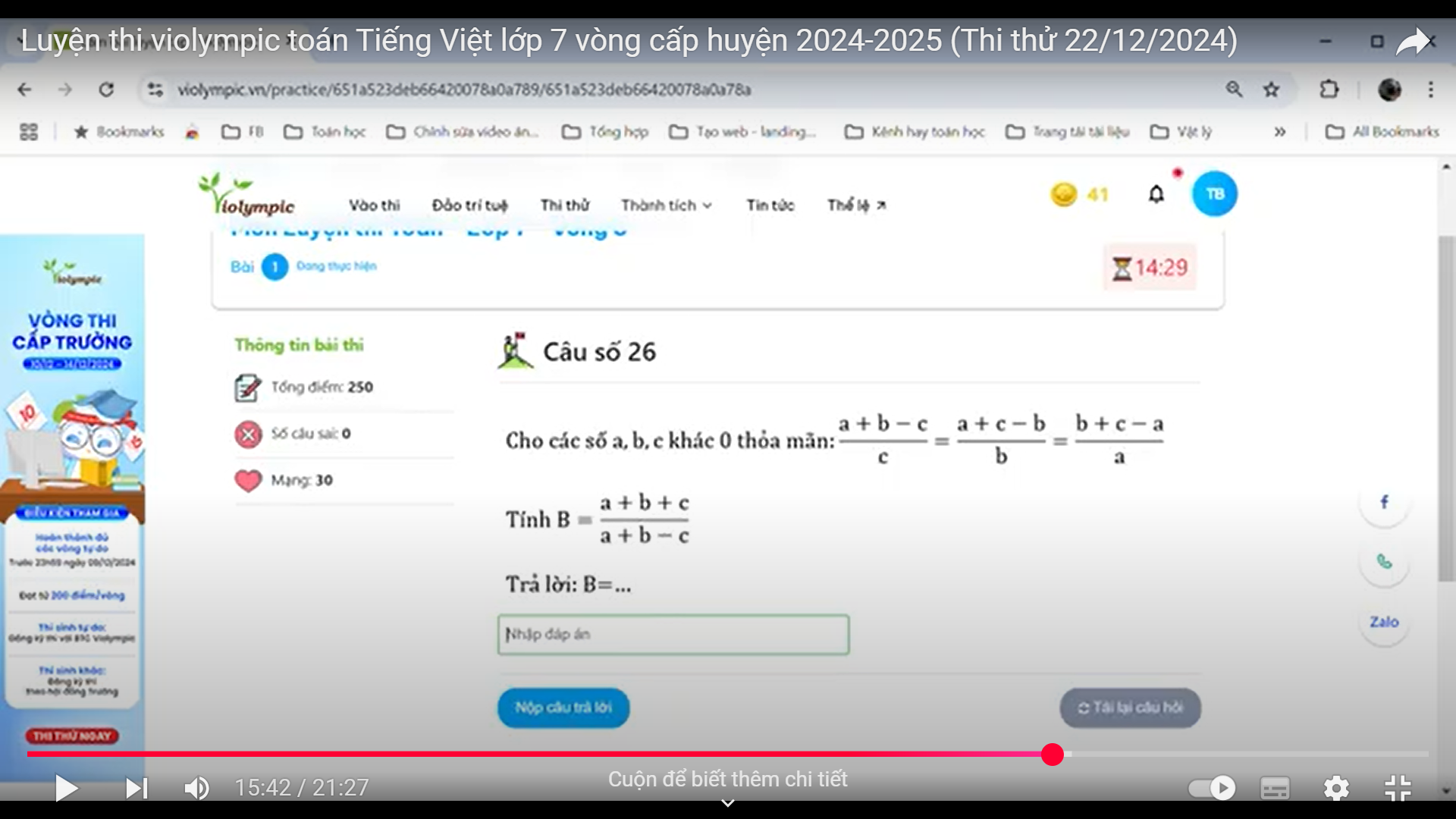
đặt \(k=\dfrac{a+b-c}{c}=\dfrac{a+c-b}{b}=\dfrac{b+c-a}{a}\)

từ đó ta có: a + b - c = kc; a + b - c = kb; b + c - a = ka

cộng ba vế lại ta được

(a + b - c) + (a + c - b) + (b + c - a) = kc + kb + ka

(a + b + c) = k(a + b + c)

mà a; b; c ≠ 0; => k = 1

nên ta có: \(a+b-c=c⇒a+b=2c\\ a+c-b=b⇒a+c=2b\\ b+c-a=a⇒b+c=2a\)

\(B=\dfrac{a+b+c}{a+b-c}=\dfrac{2c+c}{2c-c}=\dfrac{3c}{c}=3\)

vậy B = 3