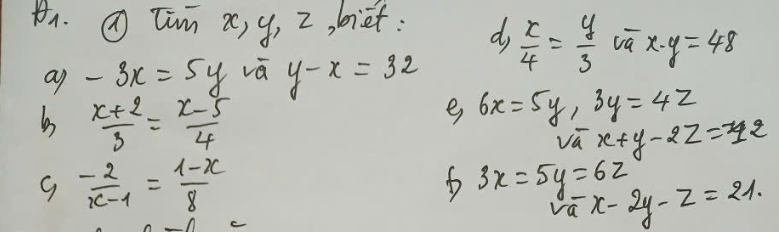a: -3x=5y
=>\(\dfrac{x}{5}=\dfrac{y}{-3}\)
mà y-x=32
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{-3}=\dfrac{y-x}{-3-5}=\dfrac{32}{-8}=-4\)
=>\(\left\{{}\begin{matrix}x=-4\cdot5=-20\\y=\left(-4\right)\cdot\left(-3\right)=12\end{matrix}\right.\)
b: \(\dfrac{x+2}{3}=\dfrac{x-5}{4}\)
=>\(4\left(x+2\right)=3\left(x-5\right)\)
=>4x+8=3x-15
=>4x-3x=-15-8
=>x=-23
c: ĐKXĐ: x<>1
\(\dfrac{-2}{x-1}=\dfrac{1-x}{8}\)
=>\(\dfrac{2}{x-1}=\dfrac{x-1}{8}\)
=>\(\left(x-1\right)^2=2\cdot8=16\)
=>\(\left[{}\begin{matrix}x-1=4\\x-1=-4\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=4+1=5\left(nhận\right)\\x=-4+1=-3\left(nhận\right)\end{matrix}\right.\)
d: Đặt \(\dfrac{x}{4}=\dfrac{y}{3}=k\)
=>x=4k; y=3k
xy=48
=>\(4k\cdot3k=48\)
=>\(12k^2=48\)
=>\(k^2=4\)
=>\(\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\)
TH1: k=2
=>\(\left\{{}\begin{matrix}x=4\cdot2=8\\y=3\cdot2=6\end{matrix}\right.\)
TH2: k=-2
=>\(\left\{{}\begin{matrix}x=4\cdot\left(-2\right)=-8\\y=3\cdot\left(-2\right)=-6\end{matrix}\right.\)
e: 6x=5y
=>\(\dfrac{x}{5}=\dfrac{y}{6}\)
=>\(\dfrac{x}{10}=\dfrac{y}{12}\left(1\right)\)
3y=4z
=>\(\dfrac{y}{4}=\dfrac{z}{3}\)
=>\(\dfrac{y}{12}=\dfrac{z}{9}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{x}{10}=\dfrac{y}{12}=\dfrac{z}{9}\)
mà x+y-2z=12
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{12}=\dfrac{z}{9}=\dfrac{x+y-2z}{10+12-2\cdot9}=\dfrac{12}{4}=3\)
=>\(\left\{{}\begin{matrix}x=3\cdot10=30\\y=3\cdot12=36\\z=3\cdot9=27\end{matrix}\right.\)
f: 3x=5y=6z
=>\(\dfrac{3x}{30}=\dfrac{5y}{30}=\dfrac{6z}{30}\)
=>\(\dfrac{x}{10}=\dfrac{y}{6}=\dfrac{z}{5}\)
mà x-2y-z=21
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{6}=\dfrac{z}{5}=\dfrac{x-2y-z}{10-2\cdot6-5}=\dfrac{21}{-7}=-3\)
=>\(\left\{{}\begin{matrix}x=-3\cdot10=-30\\y=-3\cdot6=-18\\z=-3\cdot5=-15\end{matrix}\right.\)