Question

Answer 1

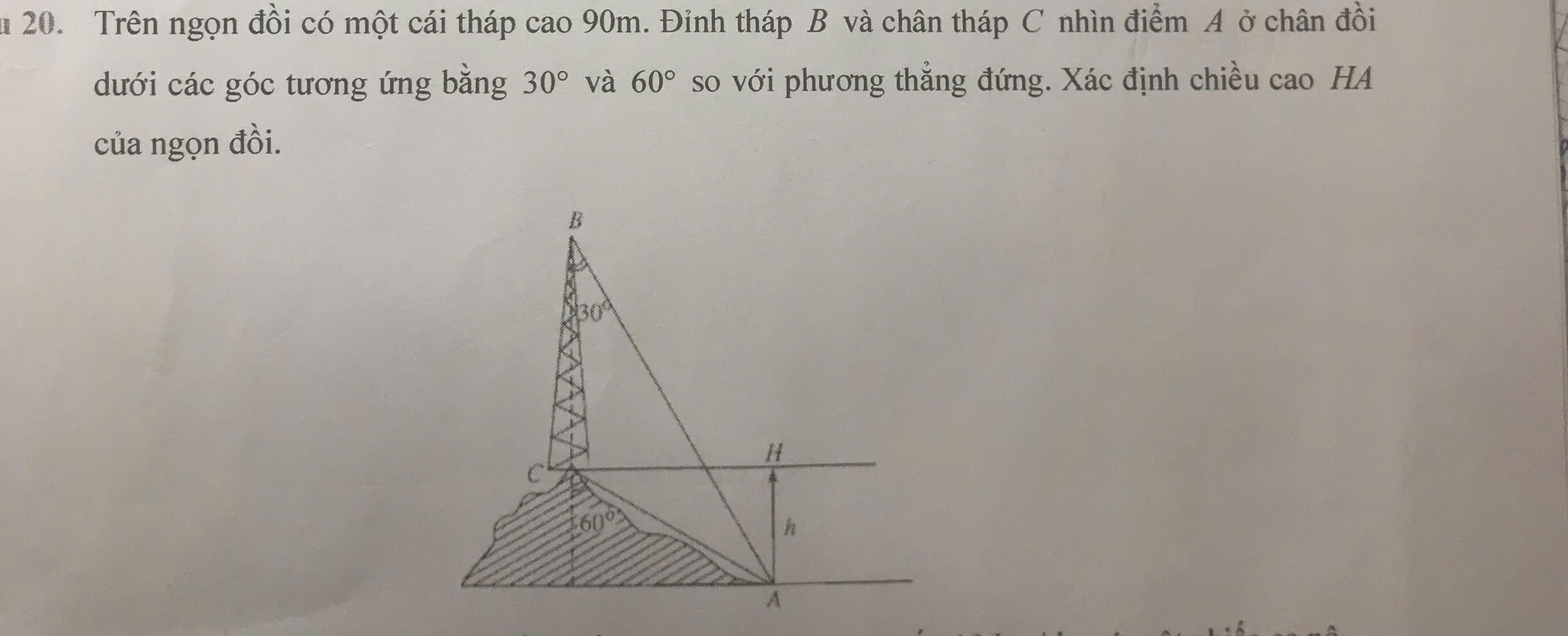
Kẻ AK⊥BC tại K

Xét tứ giác AHCK có \(\hat{AHC}=\hat{HCK}=\hat{CKA}=90^0\)

nên AHCK là hình chữ nhật

=>AH=CK và AK=CH

Xét ΔCKA vuông tại K có \(\tan ACK=\frac{AK}{CK}\)

=>\(CK=\frac{AK}{\tan ACK}=\frac{AK}{\tan60}\)

Xét ΔBCH vuông tại C có \(\tan B=\frac{CH}{CB}\)

=>\(\frac{CH}{90}=\tan30=\frac{\sqrt3}{3}\)

=>\(CH=90\cdot\frac{\sqrt3}{3}=30\sqrt3\left(m\right)\)

=>\(AK=30\sqrt3\left(m\right)\)

=>\(CK=\frac{30\sqrt3}{\tan60}=30\left(m\right)\)

=>AH=30(m)