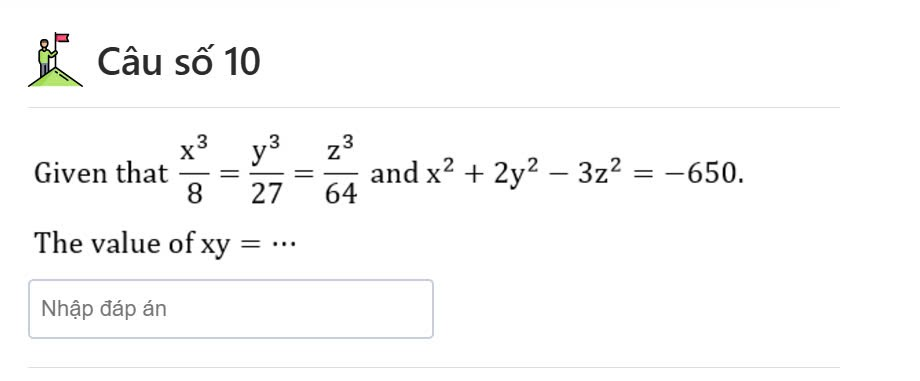Ta có: \(\dfrac{x^3}{8}=\dfrac{y^3}{27}=\dfrac{z^3}{64}\)
=>\(\left(\dfrac{x}{2}\right)^3=\left(\dfrac{y}{3}\right)^3=\left(\dfrac{z}{4}\right)^3\)
=>\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\)
Đặt \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=k\)
=>x=2k; y=3k; z=4k
\(x^2+2y^2-3z^2=-650\)
=>\(\left(2k\right)^2+2\cdot\left(3k\right)^2-3\cdot\left(4k\right)^2=-650\)
=>\(4k^2+18k^2-48k^2=-650\)
=>\(-26k^2=-650\)
=>\(k^2=25\)
=>\(\left[{}\begin{matrix}k=5\\k=-5\end{matrix}\right.\)
TH1: k=5
=>\(\left\{{}\begin{matrix}x=2\cdot5=10\\y=3\cdot5=15\end{matrix}\right.\)
\(xy=10\cdot15=150\)
TH2: k=-5
=>\(\left\{{}\begin{matrix}x=2\cdot\left(-5\right)=-10\\y=3\cdot\left(-5\right)=-15\end{matrix}\right.\)
\(xy=\left(-10\right)\cdot\left(-15\right)=150\)