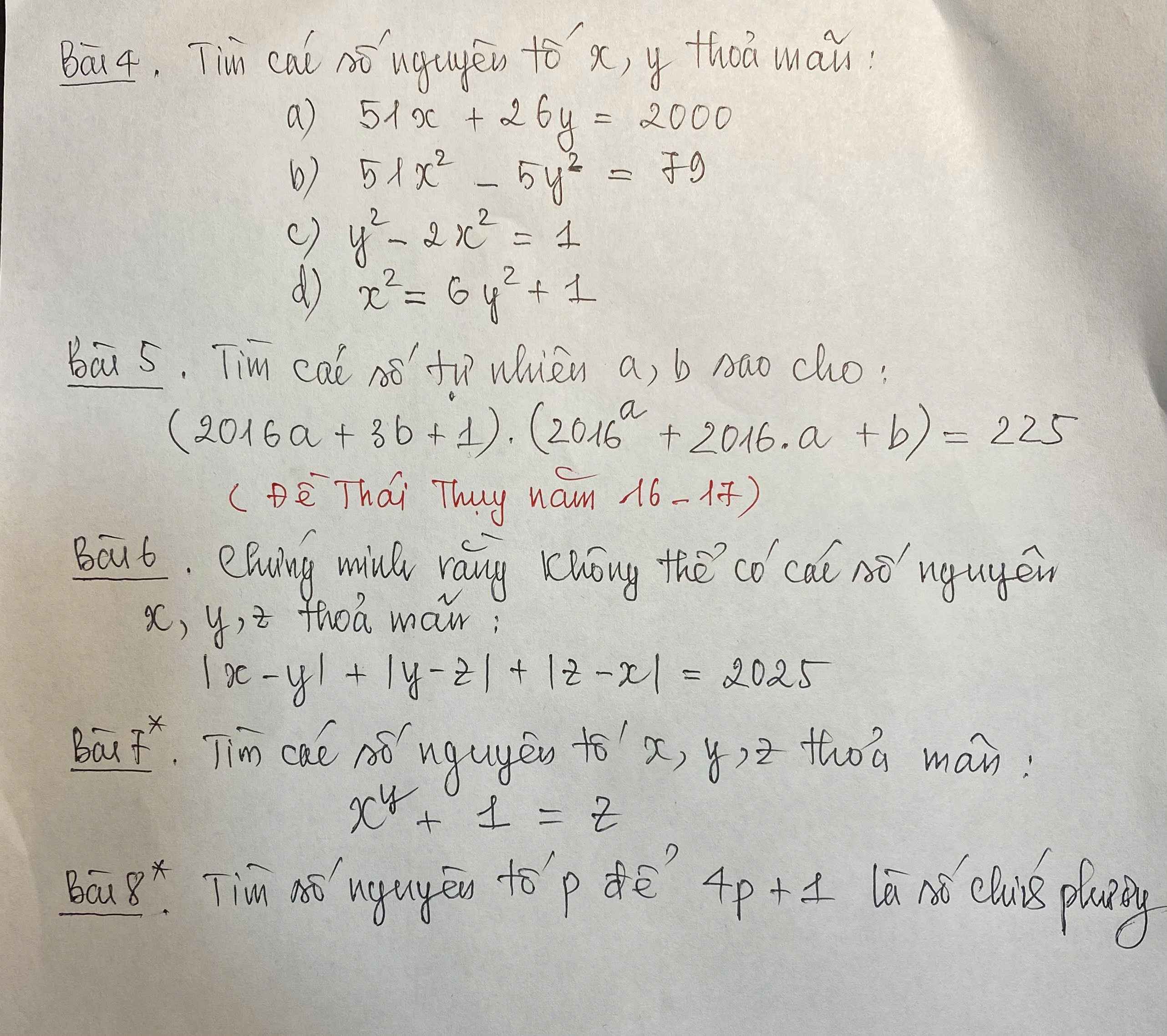Bài 8: Vì 4p+1 là số lẻ
mà 4p+1 là số chính phương
nên \(4p+1=\left(2k+1\right)^2\)
=>\(4p+1=4k^2+4k+1\)
=>\(4p=4k^2+4k=4\left(k^2+k\right)=4k\left(k+1\right)\)
=>p=k(k+1)
TH1: k=0
=>\(p=k\left(k+1\right)=0\) không là số nguyên tố
=>Loại
TH2: k=1
=>k+1=1+1=2
\(p=k\left(k+1\right)=1\cdot2=2\) là số nguyên tố
=>Nhận
TH3: k>1
=>p=k(k+1) là tích của hai số tự nhiên lớn hơn 1
=>p là hợp số
=>Loại
Vậy: p=2
Bài 4:
a: \(51x+26y=2000\)
=>\(26y=2000-51x\)
=>\(y=\frac{2000-51x}{26}\)
=>y là số chẵn
mà y là số nguyên tố
nên y=2
Ta có: 51x+26y=2000
=>\(51x=2000-26y=2000-26\cdot2=1948\)
=>\(x=\frac{1948}{51}\) không là số nguyên tố
=>Loại
Vậy: (x;y)∈∅
b: \(51x^2-5y^2=79\)
=>\(51x^2;5y^2\) khác tính chẵn lẻ
TH1: \(5y^2\) chẵn
=>\(y^2\) chẵn
=>y=2
Ta có: \(51x^2-5y^2=79\)
=>\(51x^2-5\cdot2^2=79\)
=>\(51x^2=79+20=99\)
=>\(x^2=\frac{99}{51}=\frac{33}{17}\)
mà x là số nguyên tố
nên x∈∅
=>Loại
TH2: \(51x^2\) chẵn
=>\(x^2\) chẵn
=>x=2
Ta có: \(51x^2-5y^2=79\)
=>\(5y^2=51\cdot2^2-79=125\)
=>\(y^2=25\)
=>y=5(nhận) hoặc y=-5(loại)
Vậy: x=2;y=5
c: \(y^2-2x^2=1\)
=>\(2x^2=y^2-1\)
=>\(x^2=\frac{y^2-1}{2}\)
=>\(x^2\) chẵn
mà x là số nguyên tố
nên x=2
Ta có: \(y^2-2x^2=1\)
=>\(y^2-2\cdot2^2=1\)
=>\(y^2=1+8=9\)
=>y=3(nhận) hoặc y=-3(loại)
Vậy: x=2;y=3
4: \(x^2=6y^2+1\)
=>\(6y^2=x^2-1\)
=>\(y^2=\frac{x^2-1}{6}\)
=>\(y^2\) là số chẵn
=>y là số chẵn
mà y là số nguyên tố
nên y=2
\(x^2-6y^2=1\)
=>\(x^2=6y^2+1=6\cdot2^2+1=25\)
=>x=5(nhận) hoặc x=-5(loại)
Vậy: x=5;y=2