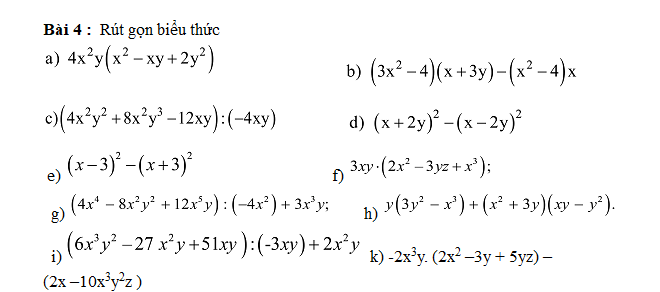a: \(4x^2y\left(x^2-xy+2y^2\right)\)
\(=4x^2y\cdot x^2-4x^2y\cdot xy+4x^2y\cdot2y^2\)
\(=4x^4y-4x^3y^2+8x^2y^3\)
b: \(\left(3x^2-4\right)\left(x+3y\right)-\left(x^2-4\right)\cdot x\)
\(=3x^3+9x^2y-4x-12y-x^3+4x\)
\(=2x^3+9x^2y-12y\)
c: \(\left(4x^2y^2+8x^2y^3-12xy\right):\left(-4xy\right)\)
\(=\dfrac{4x^2y^2}{-4xy}-\dfrac{8x^2y^3}{4xy}+\dfrac{12xy}{4xy}\)
\(=-xy-2xy^2+3\)
d: \(\left(x+2y\right)^2-\left(x-2y\right)^2\)
\(=\left(x+2y+x-2y\right)\left(x+2y-x+2y\right)\)
\(=2x\cdot4y=8xy\)
e: \(\left(x-3\right)^2-\left(x+3\right)^2\)
\(=x^2-6x+9-x^2-6x-9\)
=-12x
f: \(3xy\left(2x^2-3yz+x^3\right)\)
\(=3xy\cdot2x^2-3xy\cdot3yz+3xy\cdot x^3\)
\(=6x^3y-9xy^2z+3x^4y\)
g: \(\left(4x^4-8x^2y^2+12x^5y\right):\left(-4x^2\right)+3x^3y\)
\(=-\dfrac{4x^4}{4x^2}+\dfrac{8x^2y^2}{4x^2}-\dfrac{12x^5y}{4x^2}+3x^3y\)
\(=-x^2+2y^2-3x^3y+3x^3y=-x^2+2y^2\)
h: \(y\left(3y^2-x^3\right)+\left(x^2+3y\right)\left(xy-y^2\right)\)
\(=3y^3-x^3y+x^3y-x^2y^2+3xy^2-3y^3\)
\(=-x^2y^2+3xy^2\)
i: \(\dfrac{6x^3y^2-27x^2y+51xy}{-3xy}+2x^2y\)
\(=-\dfrac{6x^3y^2}{3xy}+\dfrac{27x^2y}{3xy}-\dfrac{51xy}{3xy}+2x^2y\)
\(=-2x^2y+9x-17+2x^2y=9x-17\)
k: \(-2x^3y\left(2x^2-3y+5yz\right)-\left(2x-10x^3y^2z\right)\)
\(=-4x^5y+6x^3y^2-10x^3y^2z-2x+10x^3y^2z\)
\(=-4x^5y+6x^3y^2-2x\)