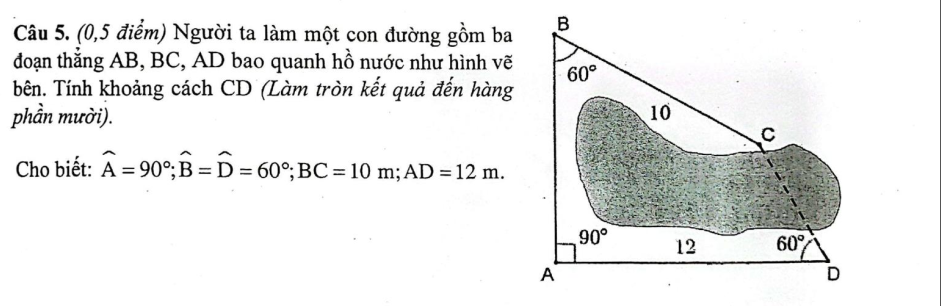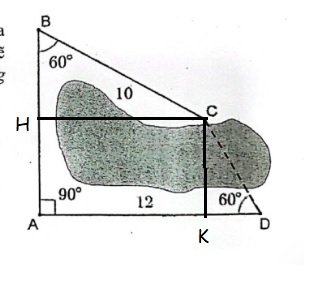
Kẻ CH vuông góc AB và CK vuông góc AD
\(\Rightarrow AHCK\) là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow AK=CH\)
Trong tam giác vuông BCH:
\(sinB=\dfrac{CH}{BC}\Rightarrow CH=BC.sinB=10.sin60^0=5\sqrt{3}\left(m\right)\)
\(\Rightarrow AK=CH=5\sqrt{3}\left(m\right)\)
\(\Rightarrow DK=AD-AK=12-5\sqrt{3}\left(m\right)\)
Trong tam giác vuông CDK:
\(cosD=\dfrac{DK}{CD}\Rightarrow CD=\dfrac{DK}{cosD}=\dfrac{12-5\sqrt{3}}{cos60^0}\approx6,7\left(m\right)\)
Đúng 1
Bình luận (0)
