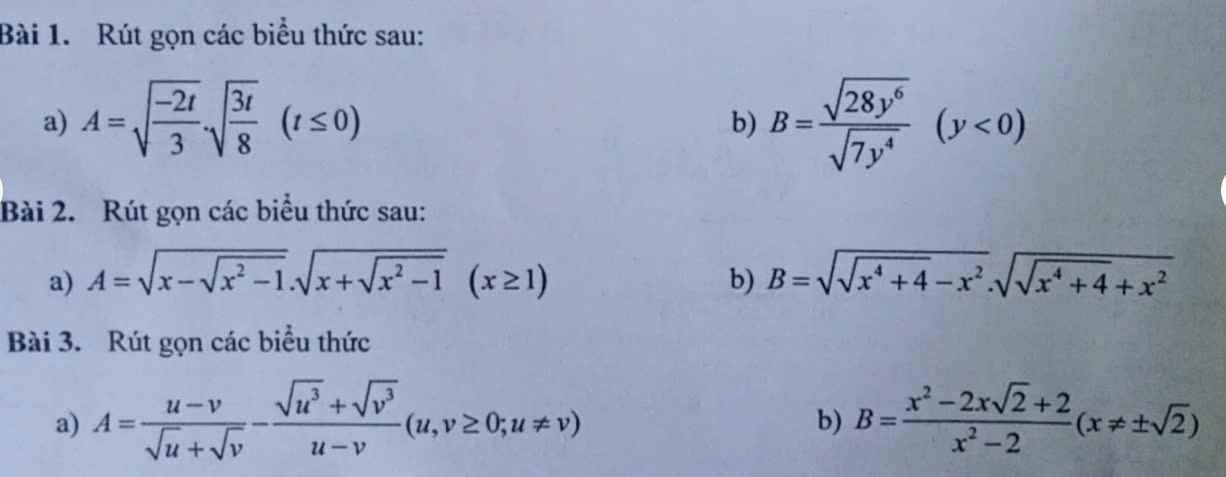1.
a. Câu này chắc đề ghi nhầm, vì nếu \(t\le0\) (1) thì để \(\sqrt{\dfrac{3t}{8}}\) xác định
\(\Rightarrow t\ge0\) (2)
(1);(2) \(\Rightarrow t=0\)
\(\Rightarrow A=0\)
b.
\(B=\dfrac{\sqrt{28y^6}}{\sqrt{7y^4}}=\dfrac{\sqrt{2^2.7.\left(y^3\right)^2}}{\sqrt{7.\left(y^2\right)^2}}=\dfrac{2\sqrt{7}.\left|y^3\right|}{\sqrt{7}.\left|y^2\right|}\)
\(=2\left|y\right|=-2y\)
2.
\(A=\sqrt{x-\sqrt{x^2-1}}.\sqrt{x+\sqrt{x^2-1}}\)
\(=\sqrt{\left(x-\sqrt{x^2-1}\right)\left(x+\sqrt{x^2-1}\right)}\)
\(=\sqrt{x^2-\left(x^2-1\right)}=\sqrt{1}=1\)
\(B=\sqrt{\sqrt{x^4+4}-x^2}.\sqrt{\sqrt{x^4+4}+x^2}\)
\(=\sqrt{\left(\sqrt{x^4+4}-x^2\right)\left(\sqrt{x^4+4}+x^2\right)}\)
\(=\sqrt{x^4+4-x^4}=\sqrt{4}=2\)
3.
\(A=\dfrac{\left(\sqrt{u}-\sqrt{v}\right)\left(\sqrt{u}+\sqrt{v}\right)}{\sqrt{u}+\sqrt{v}}-\dfrac{\left(\sqrt{u}+\sqrt{v}\right)\left(u-\sqrt{uv}+v\right)}{\left(\sqrt{u}-\sqrt{v}\right)\left(\sqrt{u}+\sqrt{v}\right)}\)
\(=\sqrt{u}-\sqrt{v}-\dfrac{u-\sqrt{uv}+v}{\sqrt{u}-\sqrt{v}}\)
\(=\dfrac{\left(\sqrt{u}-\sqrt{v}\right)^2-\left(u-\sqrt{uv}+v\right)}{\sqrt{u}-\sqrt{v}}\)
\(=\dfrac{u-2\sqrt{uv}+v-u+\sqrt{uv}-v}{\sqrt{u}-\sqrt{v}}\)
\(=\dfrac{-\sqrt{uv}}{\sqrt{u}-\sqrt{v}}\)
\(B=\dfrac{x^2-2x\sqrt{2}+2}{x^2-2}=\dfrac{\left(x-\sqrt{2}\right)^2}{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}\)
\(=\dfrac{x-\sqrt{2}}{x+\sqrt{2}}\)
1.a
\(A=\sqrt{\dfrac{-2t}{3}}.\sqrt{\dfrac{-3t}{8}}=\sqrt{\dfrac{-2t}{3}.\dfrac{\left(-3t\right)}{8}}=\sqrt{\dfrac{6t^2}{24}}\)
\(=\sqrt{\dfrac{t^2}{4}}=\sqrt{\dfrac{t^2}{2^2}}=\left|\dfrac{t}{2}\right|=-\dfrac{t}{2}\) (do \(t\le0\))