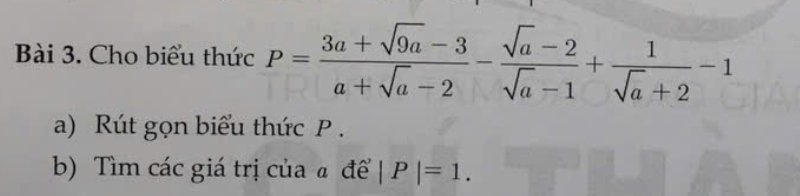a. ĐKXĐ: \(x\ge0;x\ne1\)
\(P=\dfrac{3a+3\sqrt{a}-3}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+2\right)}-\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+2\right)}+\dfrac{\sqrt{a}-1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+2\right)}-1\)
\(=\dfrac{3a+3\sqrt{a}-3-\left(a-4\right)+\sqrt{a}-1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+2\right)}-1\)
\(=\dfrac{2a+4\sqrt{a}}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+2\right)}-1\)
\(=\dfrac{2\sqrt{a}\left(\sqrt{a}+2\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+2\right)}-1=\dfrac{2\sqrt{a}}{\sqrt{a}-1}-1\)
\(=\dfrac{2\sqrt{a}-\left(\sqrt{a}-1\right)}{\sqrt{a}-1}=\dfrac{\sqrt{a}+1}{\sqrt{a}-1}\)
b.
\(\left|P\right|=1\Rightarrow\left[{}\begin{matrix}P=1\\P=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{\sqrt{a}+1}{\sqrt{a}-1}=1\\\dfrac{\sqrt{a}+1}{\sqrt{a}-1}=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\sqrt{a}+1=\sqrt{a}-1\\\sqrt{a}+1=-\sqrt{a}+1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}1=-1\left(vô-nghiệm\right)\\2\sqrt{a}=0\end{matrix}\right.\)
\(\Rightarrow\sqrt{a}=0\Rightarrow a=0\)