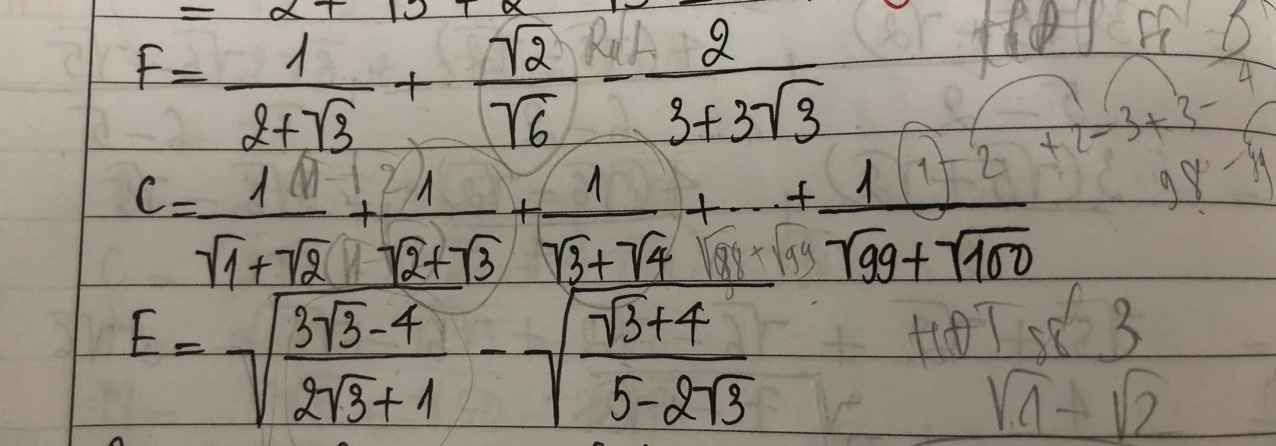\(F=\dfrac{2-\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}+\dfrac{\sqrt{2}.\sqrt{6}}{\sqrt{6}.\sqrt{6}}-\dfrac{2.\left(\sqrt{3}-1\right)}{3\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}\)
\(=\dfrac{2-\sqrt{3}}{4-3}+\dfrac{\sqrt{12}}{6}-\dfrac{2\sqrt{3}-2}{3\left(3-1\right)}\)
\(=\dfrac{12-6\sqrt{3}}{6}+\dfrac{2\sqrt{3}}{6}-\dfrac{2\sqrt{3}-2}{6}=\dfrac{14-6\sqrt{3}}{6}\)
\(=\dfrac{7-3\sqrt{3}}{3}\)
\(C=\dfrac{1-\sqrt{2}}{\left(1+\sqrt{2}\right)\left(1-\sqrt{2}\right)}+\dfrac{\sqrt{2}-\sqrt{3}}{\left(\sqrt{2}-\sqrt{3}\right)\left(\sqrt{2}+\sqrt{3}\right)}+...+\dfrac{\sqrt{99}-\sqrt{100}}{\left(\sqrt{99}-\sqrt{100}\right)\left(\sqrt{99}+\sqrt{100}\right)}\)
\(=\dfrac{1-\sqrt{2}}{-1}+\dfrac{\sqrt{2}-\sqrt{3}}{-1}+...+\dfrac{\sqrt{99}-\sqrt{100}}{-1}\)
\(=\dfrac{1-\sqrt{100}}{-1}=\dfrac{1-10}{-1}=9\)
\(E=\sqrt{\dfrac{3\sqrt{3}-4}{2\sqrt{3}+1}}-\sqrt{\dfrac{\sqrt{3}+4}{5-2\sqrt{3}}}\)
\(=\sqrt{\dfrac{\left(3\sqrt{3}-4\right)\left(2\sqrt{3}-1\right)}{\left(2\sqrt{3}+1\right)\left(2\sqrt{3}-1\right)}}-\sqrt{\dfrac{\left(\sqrt{3}+4\right)\left(5+2\sqrt{3}\right)}{\left(5-2\sqrt{3}\right)\left(5+2\sqrt{3}\right)}}\)
\(=\sqrt{\dfrac{22-11\sqrt{3}}{11}}-\sqrt{\dfrac{26+13\sqrt{3}}{13}}\)
\(=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{3}-1-\sqrt{3}-1\right)=\dfrac{-2}{\sqrt{2}}=-\sqrt{2}\)