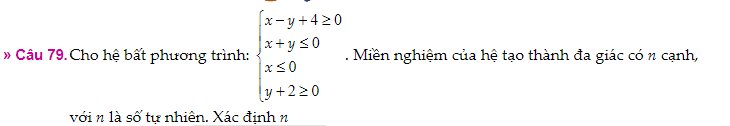Thay x=0 và y=0 vào x-y+4>=0, ta được:
0-0+4>=0
=>4>=0(đúng)
=>Miền nghiệm của bất phương trình x-y+4>=0 sẽ là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0) của đường thẳng x-y+4=0(1)
Thay x=1 và y=1 vào x+y<=0, ta được:
1+1<=0
=>-2<=0(sai)
=>Miền nghiệm của bất phương trình x+y<=0 sẽ là nửa mặt phẳng chứa biên nhưng không chứa điểm A(1;1) của đường thẳng x+y=0(2)
Vì x<=0
nên miền nghiệm của bất phương trình x<=0 sẽ là nửa mặt phẳng phần bên trái kèm theo biên của trục Oy(3)
Thay x=0;y=-2 vào y+2>=0, ta được:
-2+2>=0
=>0>=0(đúng)
=>Miền nghiệm của bất phương trình y+2>=0 sẽ là nửa mặt phẳng vừa chứa biên vừa chứa điểm B(0;-2) của đường thẳng y+2=0(4)
Từ (1),(2),(3),(4) ta có miền nghiệm của hệ bất phương trình là:
=>Miền nghiệm của hệ chính là ΔABC, với A là giao điểm của x-y+4=0 và x+y=0; B là giao điểm của y+2=0 và x-y+4=0; C là giao điểm của hai đường thẳng y+2=0 và x+y=0
=>Miền nghiệm của hệ có 3 cạnh
=>n=3