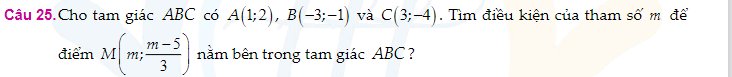\(\overrightarrow{AB}=\left(-4;-3\right)\Rightarrow\overrightarrow{n_P}=\left(3;-4\right)\)
\(\Rightarrow\left(AB\right):3\left(x-1\right)-4\left(y-2\right)=0\)
\(\Rightarrow\left(AB\right):3x-4y+5=0\)
\(\overrightarrow{AC}=\left(2;-6\right)\Rightarrow\overrightarrow{n_P}=\left(6;2\right)=2\left(3;1\right)\)
\(\Rightarrow\left(AC\right):3\left(x-1\right)+\left(y-2\right)=0\)
\(\Rightarrow\left(AC\right):3x+y-5=0\)
\(\overrightarrow{BC}=\left(6;-3\right)\Rightarrow\overrightarrow{n_P}=\left(3;6\right)=3\left(1;2\right)\)
\(\Rightarrow\left(BC\right):x+3+2\left(y+1\right)=0\)
\(\Rightarrow\left(BC\right):x+2y+5=0\)
Để \(M\) nằm trong \(\Delta ABC\) khi và chỉ khi :
- \(M\&A\) nằm cùng phía với \(BC\)
- \(M\&B\) nằm cùng phía với \(\text{AC}\)
- \(M\&C\) nằm cùng phía với \(\text{ AB}\)
Nên \(M\left(m;\dfrac{m-5}{3}\right)\) nằm trong miền nghiệm
\(\Leftrightarrow\left\{{}\begin{matrix}3x-4y+5>0\\x+2y+5>0\\3x+y-5< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3m-\dfrac{4\left(m-5\right)}{3}+5>0\\m+\dfrac{2\left(m-5\right)}{3}+5>0\\3m+\dfrac{\left(m-5\right)}{3}-5< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5m+35>0\\5m+5>0\\10m-20< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>-7\\m>-1\\m< 2\end{matrix}\right.\) \(\Leftrightarrow-1< m< 2\)
Vậy \(-1< m< 2\) thỏa mãn đề bài