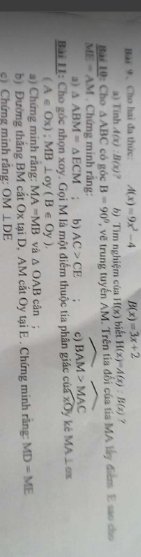Bài 11:
a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOAM=ΔOBM
=>MA=MB và OA=OB
Xét ΔOAB có OA=OB
nên ΔOAB cân tại O
b: Xét ΔMAD vuông tại A và ΔMBE vuông tại B có
MA=MB
\(\widehat{AMD}=\widehat{BME}\)(hai góc đối đỉnh)
Do đó: ΔMAD=ΔMBE
=>MD=ME
c: Ta có: ΔMAD=ΔMBE
=>AD=BE
Ta có: OA+AD=OD
OB+BE=OE
mà OA=OB và AD=BE
nên OD=OE
=>O nằm trên đường trung trực của DE(1)
Ta có: MD=ME
=>M nằm trên đường trung trực của DE(2)
Từ (1),(2) suy ra OM là đường trung trực của DE
=>OM\(\perp\)DE
Bài 10:
a: Xét ΔMBA và ΔMCE có
MB=MC
\(\widehat{BMA}=\widehat{CME}\)(hai góc đối đỉnh)
MA=ME
Do đó: ΔMBA=ΔMCE
b: Ta có: ΔMBA=ΔMCE
=>BA=CE
mà BA<AC(ΔBAC vuông tại B)
nên CE<CA
c: Xét ΔCEA có CE<CA
mà \(\widehat{CAE};\widehat{CEA}\) lần lượt là góc đối diện của các cạnh CE,CA
nên \(\widehat{CAE}< \widehat{CEA}\)
mà \(\widehat{CEA}=\widehat{BAE}\)(ΔMAB=ΔMEC)
nên \(\widehat{CAE}< \widehat{BAE}\)