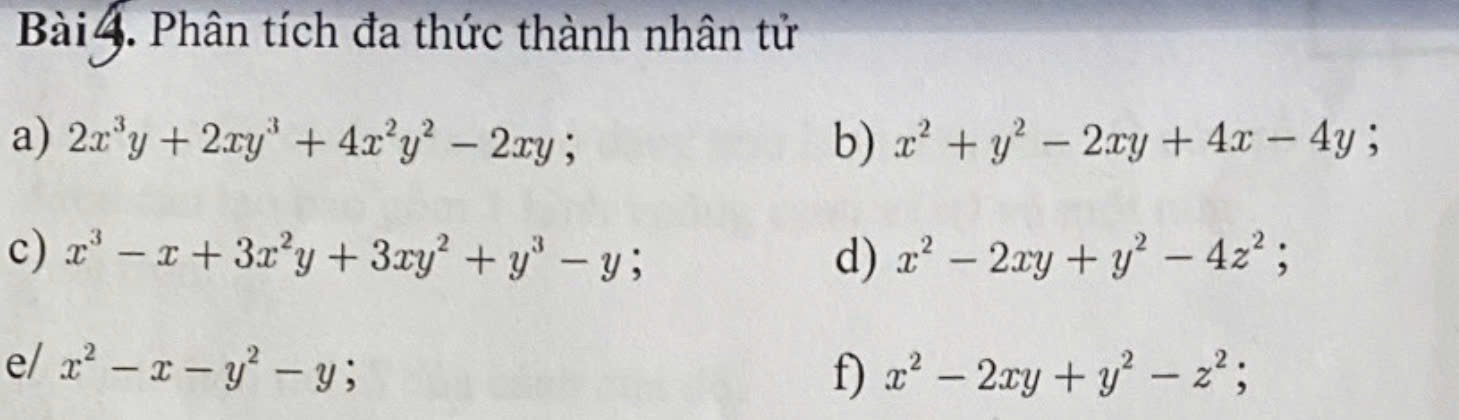\(a,2x^3y+2xy^3+4x^2y^2-2xy\\ =2xy\left[\left(x^2+y^2+2xy\right)-1\right]\\ =2xy\left[\left(x+y\right)^2-1\right]2xy\left(x+y-1\right)\left(x+y+1\right)\\ b,x^2+y^2-2xy+4x-4y\\ =\left(x^2-2xy+y^2\right)+4\left(x-y\right)\\ =\left(x-y\right)^2+4\left(x-y\right)\\ =\left(x-y\right)\left(x-y+4\right)\\ c,x^3-x+3x^2y+3xy^2+y^3-y\\ =\left(x^3+3x^2y+3xy^2+y^3\right)-\left(x+y\right)\\ =\left(x+y\right)^3-\left(x+y\right)\\ =\left(x+y\right)\left[\left(x+y\right)^2-1\right]\\=\left(x+y\right)\left(x+y+1\right)\left(x+y-1\right)\)
\(d,x^2-2xy+y^2-4z^2\\ =\left(x^2-2xy+y^2\right)-4z^2\\ =\left(x-y\right)^2-\left(2z\right)^2\\ =\left(x-y-2z\right)\left(x-y+2z\right)\\ e,x^2-x-y^2-y\\ =\left(x^2-y^2\right)-\left(x+y\right)\\ =\left(x+y\right)\left(x-y\right)-\left(x+y\right)\\ =\left(x+y\right)\left(x-y-1\right)\\ f,x^2-2xy+y^2-z^2\\ =\left(x^2-2xy+y^2\right)-z^2\\ =\left(x-y\right)^2-z^2\\ =\left(x-y-z\right)\left(x-y+z\right)\)