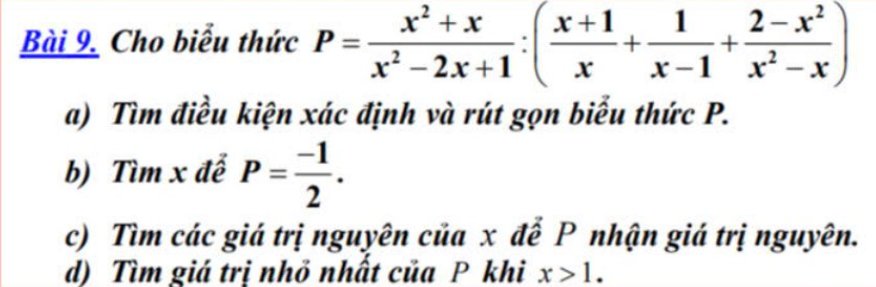\(a,ĐK:x\ne1;x\ne0\\ P=\dfrac{x^2+x}{x^2-2x+1}:\left(\dfrac{x+1}{x}+\dfrac{1}{x-1}+\dfrac{2-x^2}{x^2-x}\right)\\ =\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\left[\dfrac{\left(x+1\right)\left(x-1\right)}{x\left(x-1\right)}+\dfrac{x}{x\left(x-1\right)}+\dfrac{2-x^2}{x\left(x-1\right)}\right]\\ =\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\dfrac{x^2-1+x+2-x^2}{x\left(x-1\right)}\\ =\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\dfrac{x+1}{x\left(x-1\right)}\\ =\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}\cdot\dfrac{x\left(x-1\right)}{x+1}\\ =\dfrac{x^2}{x-1}\)
b) \(P=\dfrac{-1}{2}=>\dfrac{x^2}{x-1}=\dfrac{-1}{2}=>2x^2=1-x=>2x^2+x-1=0\)
\(=>\left(2x^2+2x\right)+\left(-x-1\right)=0\\ =>2x\left(x+1\right)-\left(x+1\right)=0\\ =>\left(2x-1\right)\left(x+1\right)=0\\ =>\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-1\end{matrix}\right.\)
c) \(P=\dfrac{x^2}{x-1}\) nguyên khi:
`x^2` ⋮ x - 1
`=>(x^2-1)+1` ⋮ x - 1
`=>(x+1)(x-1)+1` ⋮ x - 1
`=>1` ⋮ x - 1
=> x - 1 ∈ Ư(1) = {1; -1}
=> x ∈ {2; 0}
d) `x>1=>x-1>0`
`=>P=x^2/(x-1)>=0` với mọi x vì `x^2>=0`
Dấu "=" xảy ra: `x=0`