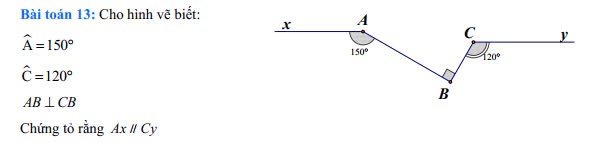
bài 13
kẻ `zt` // `Cy` (`B` thuộc `zt`)
`=>`\(\widehat{BCy}+\widehat{CBt}=180^0\)(2 góc trong cùng phía)
`=>`\(120^0+\widehat{CBt}=180^0\)
`=>`\(\widehat{CBt}=180^0-120^0=60^0\)
Có :\(\widehat{CBt}+\widehat{ABC}+\widehat{ABz}=180^0\)
`=>`\(60^0+90^0+\widehat{ABz}=180^0\)
`=>`\(\widehat{ABz}=180^0-90^0-60^0=30^0\)
Lại có :\(\widehat{xAB}+\widehat{ABz}=150^0+30^0=180^0\)
Mà 2 góc ở vị trí trong cùng phía
`=> Ax` // `zt`
Mà `zt` // Cy`
`=> Ax` // `Cy`
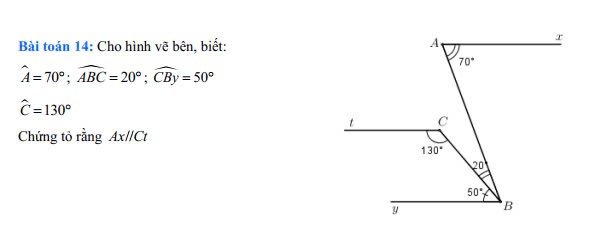
Bài 14
Có : \(\widehat{ABC}+\widehat{CBy}=20^0+50^0=70^0\)
`=>` \(\widehat{ABy}=\widehat{BAx}=70^0\)
Mà 2 góc ở vị trí so le trong
`=> Ax ` // `By (1)`
Lại có :
\(\widehat{tCB}+\widehat{CBy}=130^0+50^0=180^0\)
Mà 2 góc ở vị trí trong cùng phía
`=> tC` // `By (2)`
Từ `(1) ; (2)` suy ra `Ax` // `tC`
Kẻ `Nt` // `Tz`
`=> `\(\widehat{NTz}=\widehat{TNt}=90^0\)( so le trong)
Có : \(\widehat{TNt}+\widehat{tNM}=120^0\)
`=>`\(90^0+\widehat{tNM}=120^0\)
`=>`\(\widehat{tNM}=120^0-90^0=30^0\)
Lại có :
\(\widehat{tNM}+\widehat{NMu}=30^0+150^0=180^0\)
Mà 2 góc ở vị trí trong cùng phía
`=> Nt` // `Mu`
Mà `Nt` // `Tz`
`=> Tz` // `Mu`