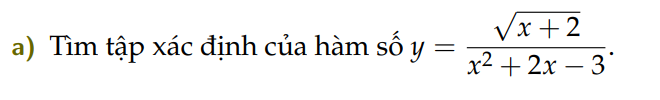Question

Answer 1

\(y=\dfrac{\sqrt{x+2}}{x^2+2x-3}\) xác định khi và chỉ khi

\(\left\{{}\begin{matrix}x+2\ge0\\x^2+2x-3\ne0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-2\\\left(x-1\right)\left(x+3\right)\ne0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-2\\x\ne1\cap x\ne-3\end{matrix}\right.\)

Tập xác định \(D=[-2;+\infty)\)\\(\left\{1;-3\right\}\)

Answer 2

\(y=\dfrac{\sqrt{x+2}}{x^2+2x-3}\)

Hàm số XĐ khi:

\(x+2\ge0\) và \(x^2+2x-3\ne0\)

\(\Leftrightarrow x\ge-2\) và \(x\ne1,x\ne3\)

Vậy..