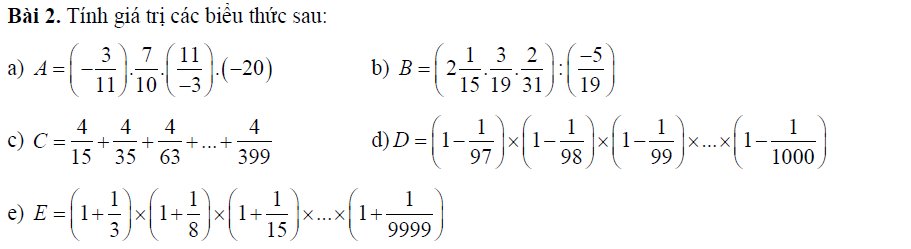C = \(\dfrac{4}{15}+\dfrac{4}{35}+\dfrac{4}{63}+...+\dfrac{4}{399}\)
C = \(\dfrac{4}{3.5}+\dfrac{4}{5.7}+\dfrac{4}{7.9}+...+\dfrac{4}{19.21}\)
2C= \(4.\left(\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{19.21}\right)\)
2C= \(4.\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{19}-\dfrac{1}{21}\right)\)
2C= \(4.\left(\dfrac{1}{3}-\dfrac{1}{21}\right)\)
2C= \(4.\left(\dfrac{7}{21}-\dfrac{1}{21}\right)\)
2C= \(4.\dfrac{6}{21}\)
2C= \(\dfrac{8}{7}\)
C= \(\dfrac{8}{7}:2\)
C= \(\dfrac{8}{7}.\dfrac{1}{2}\)
C= \(\dfrac{4}{7}\)
a: \(A=\left(-\dfrac{3}{11}\right)\cdot\dfrac{7}{10}\cdot\dfrac{11}{-3}\cdot\left(-20\right)\)
\(=\dfrac{-3}{11}\cdot\dfrac{11}{-3}\cdot\dfrac{7}{10}\cdot\left(-20\right)\)
\(=-20\cdot\dfrac{7}{10}=-14\)
b: \(B=\left(2\dfrac{1}{15}\cdot\dfrac{3}{19}\cdot\dfrac{2}{31}\right):\left(-\dfrac{5}{19}\right)\)
\(=\dfrac{31}{15}\cdot\dfrac{2}{31}\cdot\dfrac{3}{19}\cdot\dfrac{-19}{5}\)
\(=\dfrac{2}{15}\cdot\dfrac{-3}{5}=\dfrac{-6}{75}=-\dfrac{2}{25}\)
c: \(C=\dfrac{4}{15}+\dfrac{4}{35}+...+\dfrac{4}{399}\)
\(=2\left(\dfrac{2}{15}+\dfrac{2}{35}+...+\dfrac{2}{399}\right)\)
\(=2\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{19}-\dfrac{1}{21}\right)\)
\(=2\left(\dfrac{1}{3}-\dfrac{1}{21}\right)=2\cdot\dfrac{6}{21}=\dfrac{18}{21}=\dfrac{6}{7}\)
d: \(D=\left(1-\dfrac{1}{97}\right)\cdot\left(1-\dfrac{1}{98}\right)\cdot...\cdot\left(1-\dfrac{1}{1000}\right)\)
\(=\dfrac{96}{97}\cdot\dfrac{97}{98}\cdot...\cdot\dfrac{999}{1000}\)
\(=\dfrac{96}{1000}=\dfrac{12}{125}\)
e: \(E=\left(1+\dfrac{1}{3}\right)\cdot\left(1+\dfrac{1}{8}\right)\cdot...\cdot\left(1+\dfrac{1}{9999}\right)\)
\(=\left(1+\dfrac{1}{2^2-1}\right)\cdot\left(1+\dfrac{1}{3^2-1}\right)\cdot...\cdot\left(1+\dfrac{1}{100^2-1}\right)\)
\(=\dfrac{2^2}{2^2-1}\cdot\dfrac{3^2}{3^2-1}\cdot...\cdot\dfrac{100^2}{100^2-1}\)
\(=\dfrac{2\cdot3\cdot...\cdot100}{1\cdot2\cdot...\cdot100}\cdot\dfrac{2\cdot3\cdot...\cdot100}{3\cdot4\cdot...\cdot101}=\dfrac{100}{1}\cdot\dfrac{2}{101}=\dfrac{200}{101}\)