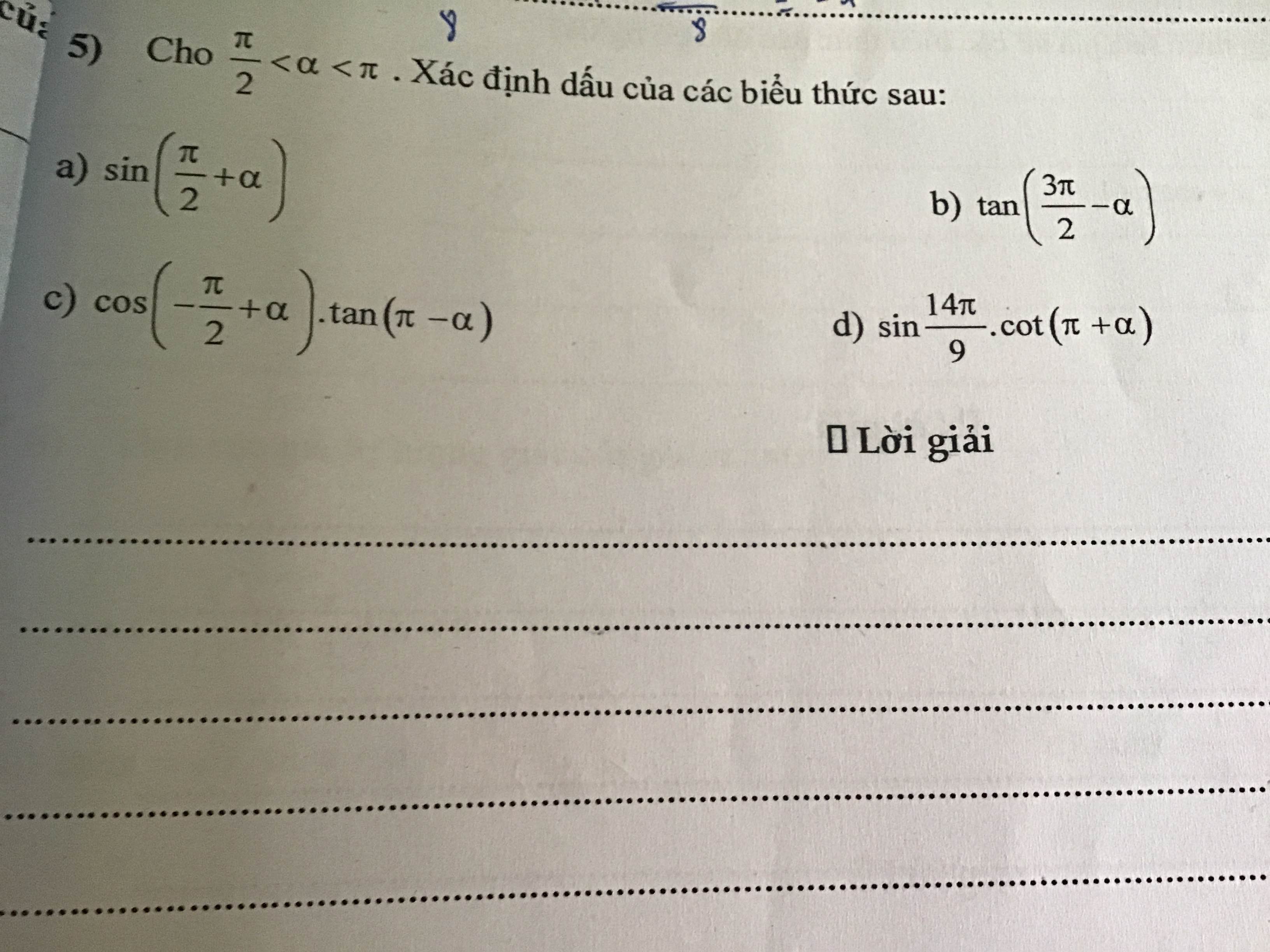a: \(\dfrac{\Omega}{2}< \alpha< \Omega\)
=>\(\dfrac{\Omega}{2}+\dfrac{\Omega}{2}< \alpha+\dfrac{\Omega}{2}< \Omega+\dfrac{\Omega}{2}\)
=>\(\Omega< \alpha+\dfrac{\Omega}{2}< \dfrac{3}{2}\Omega\)
=>\(sin\left(\dfrac{\Omega}{2}+\alpha\right)< 0\)
b: \(\dfrac{\Omega}{2}< \alpha< \Omega\)
=>\(-\dfrac{\Omega}{2}>-\alpha>-\Omega\)
=>\(-\dfrac{\Omega}{2}+\dfrac{3\Omega}{2}>-\alpha+\dfrac{3}{2}\Omega>-\Omega+\dfrac{3}{2}\Omega\)
=>\(\dfrac{1}{2}\Omega< \dfrac{3}{2}\Omega-\alpha< \Omega\)
=>\(tan\left(\dfrac{3}{2}\Omega-\alpha\right)< 0\)
c: \(\dfrac{\Omega}{2}< \alpha< \Omega\)
=>\(\dfrac{\Omega}{2}-\dfrac{\Omega}{2}< \alpha-\dfrac{\Omega}{2}< \Omega-\dfrac{\Omega}{2}\)
=>\(0< a-\dfrac{\Omega}{2}< \dfrac{\Omega}{2}\)
=>\(cos\left(\alpha-\dfrac{\Omega}{2}\right)>0\)
\(-\dfrac{\Omega}{2}>-\alpha>-\Omega\)
=>\(-\dfrac{\Omega}{2}+\Omega>-\alpha+\Omega>-\Omega+\Omega\)
=>\(\dfrac{\Omega}{2}>\Omega-\alpha>0\)
=>\(tan\left(\Omega-\alpha\right)>0\)
=>\(cos\left(-\dfrac{\Omega}{2}+\alpha\right)\cdot tan\left(\Omega-\alpha\right)>0\)
d: \(\dfrac{\Omega}{2}< \alpha< \Omega\)
=>\(\dfrac{\Omega}{2}+\Omega< \alpha+\Omega< \Omega+\Omega\)
=>\(\dfrac{3}{2}\Omega< \alpha+\Omega< 2\Omega\)
=>\(cot\left(\Omega+\alpha\right)< 0\)
\(sin\left(\dfrac{14}{9}\Omega\right)>0\)
=>\(sin\left(\dfrac{14\Omega}{9}\right)\cdot cot\left(\Omega+\alpha\right)< 0\)