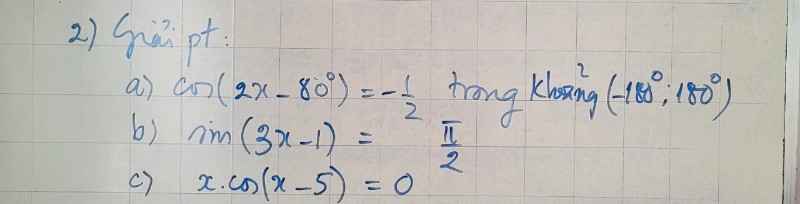a: \(cos\left(2x-80^0\right)=-\dfrac{1}{2}\)
=>\(\left[{}\begin{matrix}2x-80^0=-120^0+k\cdot360^0\\2x-80^0=120^0+k\cdot360^0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}2x=-40^0+k\cdot360^0\\2x=200^0+k\cdot360^0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-20^0+k\cdot180^0\\x=100^0+k\cdot180^0\end{matrix}\right.\)
\(x\in\left(-180^0;180^0\right)\)
=>\(\left[{}\begin{matrix}-20^0+k\cdot180^0\in\left(-180^0;180^0\right)\\100^0+k\cdot180^0\in\left(-180^0;180^0\right)\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}k\cdot180^0\in\left(-160^0;200^0\right)\\k\cdot180^0\in\left(-280^0;80^0\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}k\in\left(-\dfrac{8}{9};\dfrac{10}{9}\right)\\k\in\left(-\dfrac{14}{9};\dfrac{4}{9}\right)\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}k\in\left\{0;1\right\}\\k\in\left\{-1;0\right\}\end{matrix}\right.\)
Khi k=0 thì \(\left[{}\begin{matrix}x=-20^0+0\cdot180^0=-20^0\\x=100^0+0\cdot180^0=100^0\end{matrix}\right.\)
Khi k=1 thì \(x=-20^0+180^0=160^0\)
Khi k=-1 thì \(x=100^0-180^0=-80^0\)
b: \(sin\left(3x-1\right)=\dfrac{\Omega}{2}\)
mà \(\dfrac{\Omega}{2}>1\)
nên \(x\in\varnothing\)
c: \(x\cdot cos\left(x-5\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\cos\left(x-5\right)=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x-5=\dfrac{\Omega}{2}+k\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5+\dfrac{\Omega}{2}+k\Omega\end{matrix}\right.\)