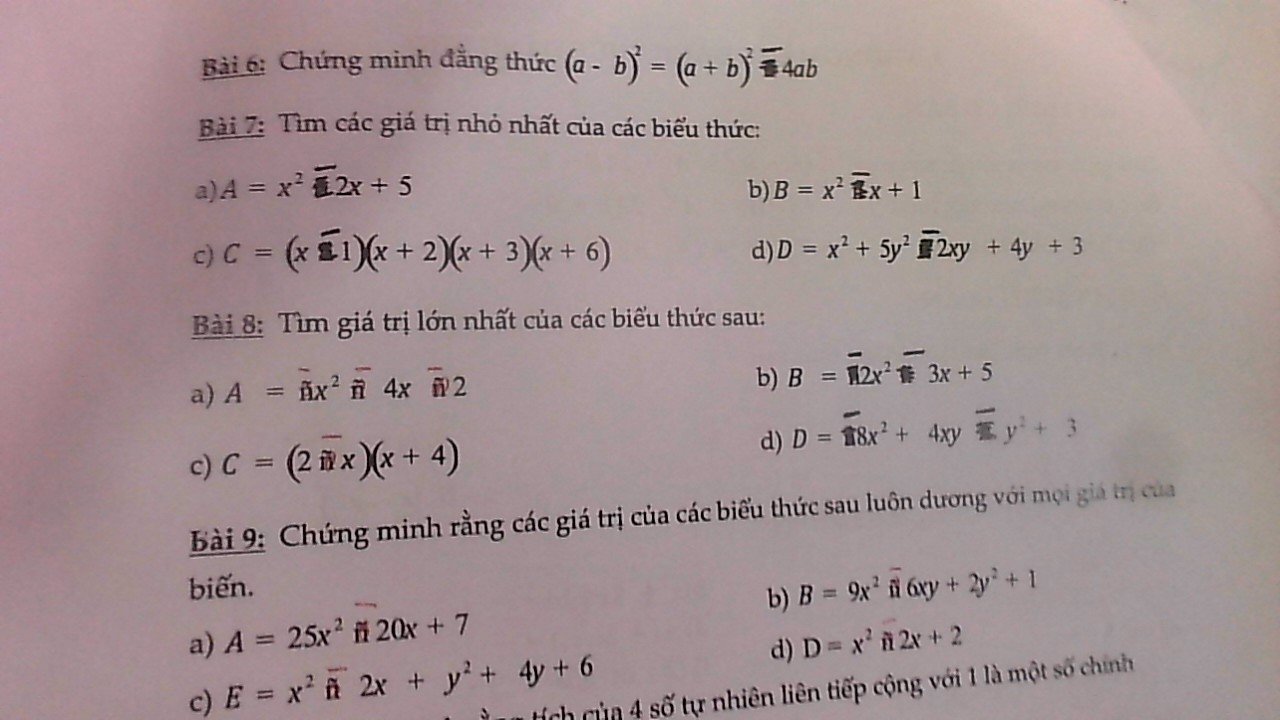Bài 7:
\(a.A=x^2-2x+5\\ =\left(x^2-2x+1\right)+4\\ =\left(x-1\right)^2+4\ge4\forall x\)
Dấu "=" xảy ra: x - 1 = 0 <=> x = 1
\(b.B=x^2-x+1\\ =\left(x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}\right)+\dfrac{3}{4}\\ =\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu "=" xảy ra: `x-1/2=0<=>x=1/2`
\(c,C=\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\\ =\left[\left(x-1\right)\left(x+6\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]\\=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\\ =\left(x^2+5x\right)^2-36\ge-36\forall x\)
Dấu "=" xảy ra: `x^2+5x=0<=>x=0` hoặc `x=-5`
\(d.D=x^2+5y^2-2xy+4y+3\\ =\left(x^2-2xy+y^2\right)+\left(4y^2+4y+1\right)+2\\ =\left(x-y\right)^2+\left(2y+1\right)^2+2\ge2\forall x,y\)
Dấu "=" xảy ra: `x-y=0` và `2y+1=0`
`=>x=y=-1/2`