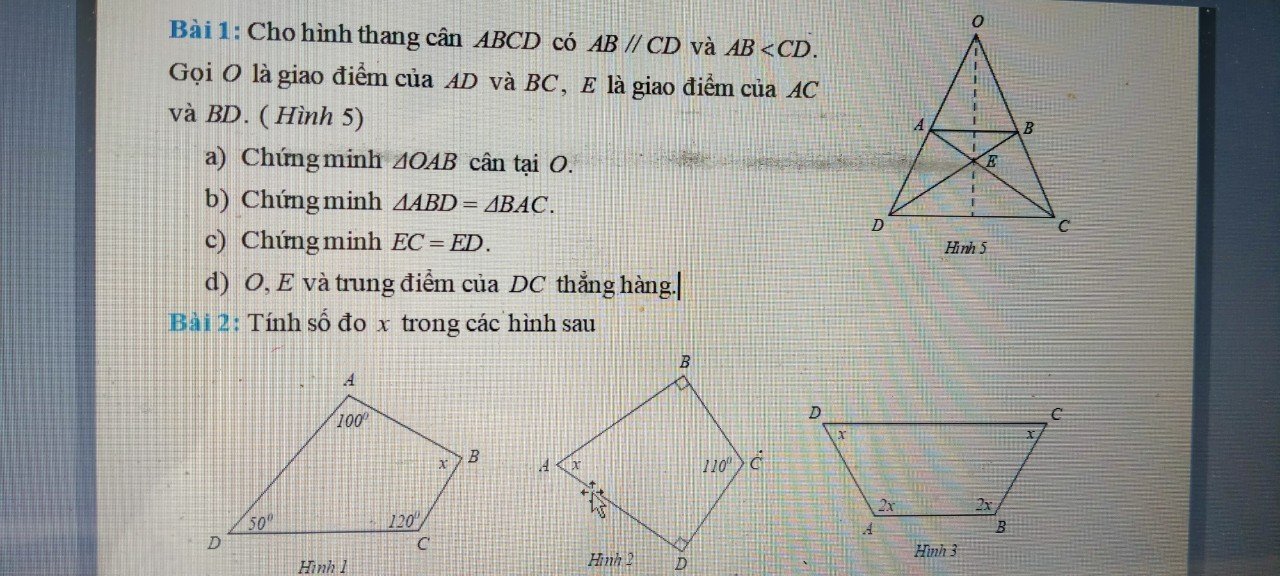
Bài 1:
a: Ta có: AB//CD
=>\(\widehat{OAB}=\widehat{ADC};\widehat{OBA}=\widehat{BCD}\)
mà \(\widehat{ADC}=\widehat{BCD}\)(ABCD là hình thang cân)
nên \(\widehat{OAB}=\widehat{OBA}\)
=>ΔOAB cân tại O
b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó:ΔABD=ΔBAC
c: Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
Do đó: ΔADC=ΔBCD
=>\(\widehat{ACD}=\widehat{BDC}\)
=>\(\widehat{ECD}=\widehat{EDC}\)
=>ΔEDC cân tại E
=>ED=EC
d: ta có: OA+AD=OD
OB+BC=OC
mà OA=OB và AD=BC
nên OD=OC
=>O nằm trên đường trung trực của DC(1)
Ta có: ED=EC
=>E nằm trên đường trung trực của DC(2)
từ (1),(2) suy ra OE là đường trung trực của DC
=>O,E,trung điểm của DC thẳng hàng
Bài 2:
Hình 1:
Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(x+100^0+120^0+50^0=360^0\)
=>\(x=90^0\)
Hình 2:
Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(x+90^0+90^0+110^0=360^0\)
=>\(x=70^0\)
Hình 3:
Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(2x+2x+x+x=360^0\)
=>\(6x=360^0\)
=>\(x=60^0\)