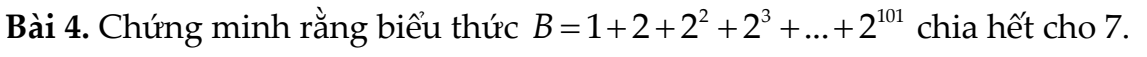Question

Answer 1

\(B=1+2+2^2+...+2^{101}\)

\(=\left(1+2+2^2\right)+\left(2^3+2^4+2^5\right)+...+\left(2^{99}+2^{100}+2^{101}\right)\)

\(=\left(1+2+2^2\right)+2^3\left(1+2+2^2\right)+...+2^{99}\left(1+2+2^2\right)\)

\(=7\left(1+2^3+...+2^{99}\right)⋮7\)

Answer 2

`B=1+2+2^2+2^3+....+2^101`

Từ `1->2^101` có 102 số số hạng nên ta chia thành 34 cặp mỗi cặp 3 số

`B=(1+2+2^2)+(2^3+2^4+2^5)+....+(2^99+2^100+2^101)`

`B=7+2^3(1+2+2^2)+...+2^99(1+2+2^2)`

`B=7(1+2^3+...+2^99)\vdots 7(dpcm)`