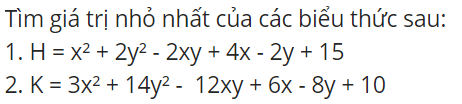1: \(H=x^2+2y^2-2xy+4x-2y+15\)
\(=x^2-2xy+4x+2y^2-2y+15\)
\(=x^2+2x\left(y-2\right)+y^2-4y+4+y^2+2y+11\)
\(=\left(x+y-2\right)^2+y^2+2y+1+10\)
\(=\left(x+y-2\right)^2+\left(y+1\right)^2+10\ge10\forall x,y\)
Dấu '=' xảy ra khi \(\begin{cases}x+y-2=0\\ y+1=0\end{cases}\Rightarrow\begin{cases}y=-1\\ x=-y+2=-\left(-1\right)+2=1+2=3\end{cases}\)
2: \(K=3x^2+14y^2-12xy+6x-8y+10\)
\(=3x^2-12xy+6x+14y^2-8y+10\)
\(=3\left(x^2-4xy+2x\right)+14y^2-8y+10\)
\(=3\left\lbrack x^2-2x\left(2y-1\right)\right\rbrack+14y^2-8y+10\)
\(=3\left\lbrack x^2-2x\left(2y-1\right)+\left(2y-1\right)^2-\left(2y-1\right)^2\right\rbrack+14y^2-8y+10\)
\(=3\left\lbrack\left(x-2y+1\right)^2\right\rbrack-3\left(2y-1\right)^2+14y^2-8y+10\)
\(=3\left(x-2y+1\right)^2-3\left(4y^2-4y+1\right)+14y^2-8y+10\)
\(=3\left(x-2y+1\right)^2-12y^2+12y-3+14y^2-8y+10\)
\(=3\left(x-2y+1\right)^2+2y^2+4y+7\)
\(=3\cdot\left(x-2y+1\right)^2+2y^2+4y+2+5\)
\(=3\left(x-2y+1\right)^2+2\left(y+1\right)^2+5\ge5\forall x,y\)
Dấu '=' xảy ra khi \(\begin{cases}x-2y+1=0\\ y+1=0\end{cases}\Rightarrow\begin{cases}y=-1\\ x=2y-1=2\cdot\left(-1\right)-1=-2-1=-3\end{cases}\)