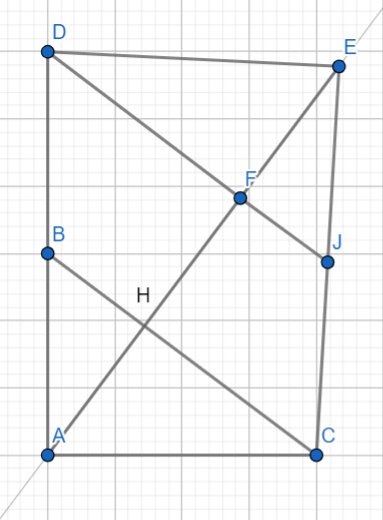
Bạn tự vẽ hình.
Ta có \(HE=2HA\) và \(HE+HA=AE\) nên \(AE=3AH\)
Do EH là trung tuyến của tam giác AED nên \(BE^2=\dfrac{AE^2+DE^2}{2}-\dfrac{AD^2}{4}=\dfrac{AE^2+DE^2}{2}-AB^2\) (chứng minh bằng cách áp dụng định lí cos trong 2 tam giác BDE và tam giác BAE).
Suy ra \(DE^2=2BE^2-AE^2+2AB^2\).
Áp dụng định lí 4 điểm cho 4 điểm A,B,C,E, ta có:
\(AB^2-AC^2=EB^2-EC^2\Rightarrow EC^2=AC^2-AB^2+EB^2\).
Thực hiện biến đổi đại số, ta có:
\(DE^2+EC^2=DE^2+AC^2-AB^2+EB^2=\left(2BE^2-AE^2+2AB^2\right)+AC^2-AB^2+EB^2=3BE^2-AE^2+AB^2+AC^2=3BH^2+3HE^2-AE^2+AB^2+AC^2=3BH^2+3.4HA^2-9HA^2+AB^2+AC^2=3\left(BH^2+AH^2\right)+AB^2+AC^2=3AB^2+AB^2+AC^2=AD^2+AC^2=DC^2\)
\(\Rightarrow\)Tam giác DEC vuông tại E (định lí Py-ta-go đảo) =>đpcm.
Kẻ \(DF\perp AE\) , cắt \(EC\) tại `J`
Xét △`AFD` có:
`AB=DB`
`BH` song song `DF`
`=>BH` là đường trung bình của △`AFD`
\(=>\left\{{}\begin{matrix}2BH=DF\\AH=HF=EF\end{matrix}\right.\)
Ta có: `AH^2=HB*HC` (theo hệ thức giữa cạnh và đường cao trong tam giác )
\(=>HC=\dfrac{AH^2}{HB}\)
`tanDEF=DF/EF`
`=>tanDEF=2BH/EF` `(1)`
`tanECH=HE/HC`
`=>tanECH=2BH/AH`
`=>tanECH=2BH/EF` `(2)`
Từ `(1)` và `(2)`
\(=>\widehat{DEF}=\widehat{ECH}\)
\(=>\widehat{DEF}+\widehat{HEC}=\widehat{ECH}+\widehat{HEC}\)
\(=>DEC=90^o\) `(đpcm)`