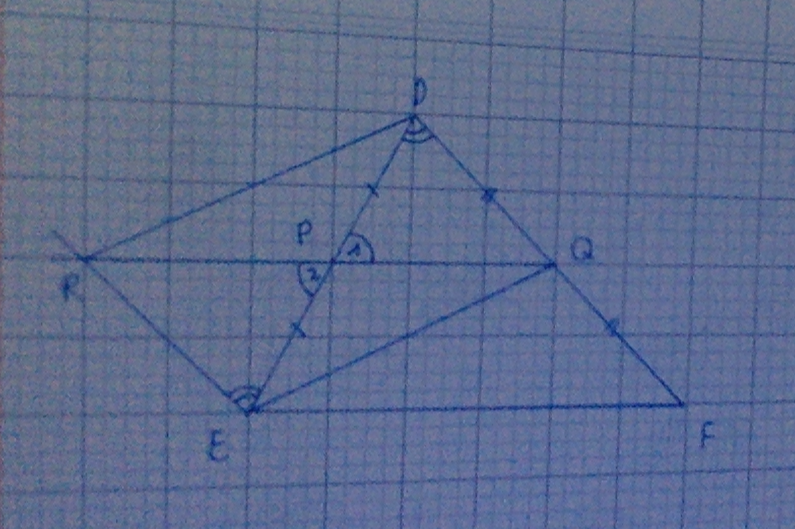
ER//DF => \(\widehat{PDQ}=\widehat{PER}\) (so le trong)
Xét \(\Delta PDQ\) và \(\Delta PER\) có \(\widehat{P_1}=\widehat{P_2}\) (đối đỉnh), \(\widehat{PDQ}=\widehat{PER}\) (cmt), PD = PE (P là trung điểm DE) nên \(\Delta PDQ=\Delta PER\left(g-c-g\right)\) \(\Rightarrow PQ=PR\) (cạnh tương ứng) => P là trung điểm QR
Tứ giác DREQ có P là trung điểm 2 đường chéo DE, QR nên là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường)
DREQ là hình bình hành nên DQ = ER => FQ = ER (DQ = FQ do Q là trung điểm DF). Tứ giác RQFE có QF = ER, QF//ER (do DF//ER) nên là hình bình hành (tứ giác có 2 cạnh đối song song và bằng nhau)
















