Bài 7:
P(x)+Q(x)
\(=x^3-2x^2+x-5-x^3+2x^2+3x-9\)
=4x-14
P(x)-Q(x)
\(=x^3-2x^2+x-5+x^3-2x^2-3x+9\)
\(=2x^3-4x^2-2x+4\)
Bài 5:
a: \(f\left(x\right)=\left(2x^2-3x+1\right)-\left(x^2-7x-2\right)\)
\(=2x^2-3x+1-x^2+7x+2\)
\(=x^2+4x+3\)
b: \(f\left(-1\right)=\left(-1\right)^2+4\cdot\left(-1\right)+3=1-4+3=0\)
=>x=-1 là nghiệm của f(x)
\(f\left(-3\right)=\left(-3\right)^2+4\cdot\left(-3\right)+3=9-12+3=0\)
=>x=-3 là nghiệm của f(x)
Bài 6:
Cách 1:
\(P\left(x\right)+Q\left(x\right)\)
\(=x^4+2x^3+x-2-2x^4-x^3+x^2+1\)
\(=-x^4+x^3+x^2+x-1\)
Cách 2: 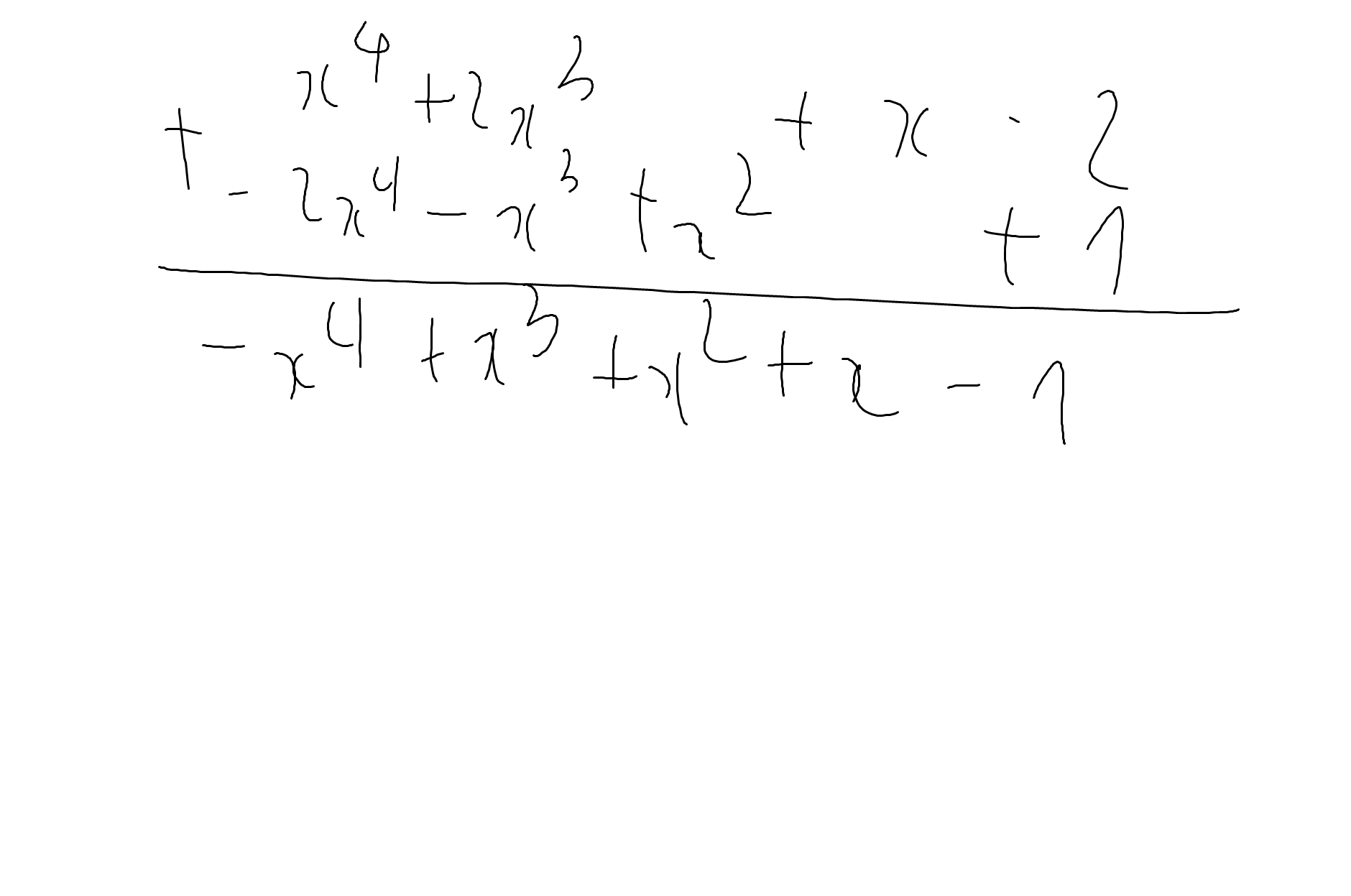
`#3107.101107`
`5.`
`a)`
\(f\left(x\right)=\left(2x^2-3x+1\right)-\left(x^2-7x-2\right)\\ =2x^2-3x+1-x^2+7x+2\\ =\left(2x^2-x^2\right)+\left(7x-3x\right)+\left(1+2\right)\\ =x^2+4x+3\)
`b)`
Thay `x = -1`
`f(-1) = (-1)^2 + 4*(-1) + 3 = 0`
`=> -1` là nghiệm của `f(x)`
Thay `x = -3`
`f(-3) = (-3)^2 + 4*(-3) + 3 = 0`
`=> -3` là nghiệm của `f(x)`
Hoặc
`x^2 + 4x + 3 = 0`
\(\Rightarrow x^2+3x+x+3=0\\ \Rightarrow\left(x^2+x\right)+\left(3x+3\right)=0\\ \Rightarrow x\left(x+1\right)+3\left(x+1\right)=0\\ \Rightarrow\left(x+3\right)\left(x+1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x+3=0\\x+1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-3\\x=-1\end{matrix}\right.\)
Vậy, nghiệm của `f(x)` là `-3; -1`
`6.`
`P(x) + Q(x) =`\(x^4+2x^3+x-2+\left(-2x^4-x^3+x^2+1\right)\)
`= x^4 - 2x^3 + x - 2 - 2x^4 - x^3 + x^2 + 1`
`= (x^4 - 2x^4) - (2x^3 + x^3) + x + (-2 + 1)`
`= -x^4 - 3x^3 + x - 1`
1 cách nữa là tính dọc á, cái này bạn tự tính cũng được nha. Nếu bạn cần thì bl xuống để mình làm thêm cho.
`7.`
`P(x) + Q(x)`
`=`\(x^3 - 2x^2 + x - 5 + (-x^3 + 2x^2 + 3x - 9)\)
`= x^3 - 2x^2 + x - 5 - x^3 + 2x^2 + 3x - 9`
`= (x^3 - x^3) - (2x^2 - 2x^2) + (x + 3x) - (5 + 9)`
`= 4x - 14`
`P(x) - Q(x)`
`= x^3 - 2x^2 + x - 5 - (-x^3 + 2x^2 + 3x - 9)`
`= x^3 - 2x^2 + x - 5 + x^3 - 2x^2 - 3x + 9`
`= (x^3 + x^3) - (2x^2 + 2x^2) + (x - 3x) + (9 - 5)`
`= 2x^3 - 4x^2 - 2x + 4`

















