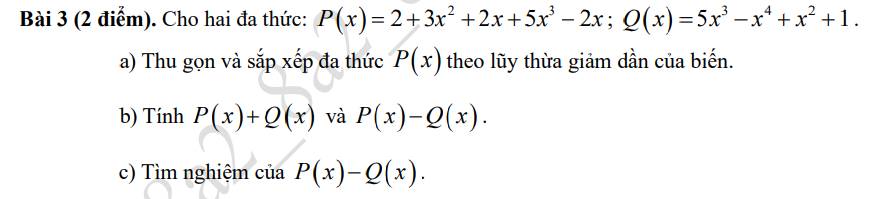a) \(P\left(x\right)=2+3x^2+2x+5x^3-2x\)
\(=5x^3+3x^2+\left(2x-2x\right)+2\)
\(=5x^3+3x^2+2\)
b) \(P\left(x\right)+Q\left(x\right)\)
\(=5x^3+3x^2+2+5x^3-x^4+x^2+1\)
\(=-x^4+10x^3+4x^2+3\)
\(P\left(x\right)-Q\left(x\right)\)
\(=\left(5x^3+3x^2+2\right)-\left(5x^3-x^4+x^2+1\right)\)
\(=5x^3+3x^2+2-5x^3+x^4-x^2-1\)
\(=x^4+2x^2+1\)
c) \(P\left(x\right)-Q\left(x\right)=x^4+2x^2+1\)
\(=\left(x^2\right)^2+2\cdot x^2\cdot1+1^2=\left(x^2+1\right)^2\)
Ta có: \(x^2\ge0\Rightarrow x^2+1\ge1\Rightarrow\left(x^2+1\right)^2\ge1^2=1>0\)
Nên P(x) - Q(x) không có nghiệm
a, \(P\left(x\right)=5x^3+3x^2+2\)
b, \(P\left(x\right)+Q\left(x\right)=5x^3+3x^2+2+5x^3-x^4+x^2+1=10x^3-x^4+4x^2+3\)
\(P\left(x\right)-Q\left(x\right)=5x^3+3x^2+2+x^4-x^2-1-5x^3=2x^2+x^4+1\)
c, Cho \(x^4+2x^2+1=0\Leftrightarrow\left(x^2+1\right)^2=0\)
Vay pt vo nghiem do x^2 + 1 > 0