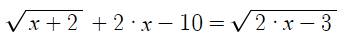đk x >= 3/2
\(\Leftrightarrow2\left(x-5\right)=\dfrac{2x-3-x-2}{\sqrt{2x-3}+\sqrt{x+2}}=\dfrac{x-5}{\sqrt{2x-3}+\sqrt{x+2}}\)
\(\Leftrightarrow\left(x-5\right)\left(\dfrac{1}{\sqrt{2x-3}+\sqrt{x+2}}-2\right)=0\)
TH1 : x = 5
TH2 : \(\dfrac{1}{\sqrt{2x-3}+\sqrt{x+2}}=2\Rightarrow1=2\sqrt{2x-3}+2\sqrt{x+2}\)
\(\Leftrightarrow\dfrac{1}{4}=3x-1+2\sqrt{\left(2x-3\right)\left(x+2\right)}\Leftrightarrow\dfrac{5}{4}-3x=2\sqrt{\left(2x-3\right)\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{25}{16}-\dfrac{15}{2}x+9x^2=4\left(2x^2+x-6\right)\)
\(\Leftrightarrow x^2-\dfrac{23}{2}x+\dfrac{409}{16}=0\Leftrightarrow x=\dfrac{23+2\sqrt{30}}{4}\left(tm\right);\dfrac{23-2\sqrt{30}}{4}\left(tm\right)\)