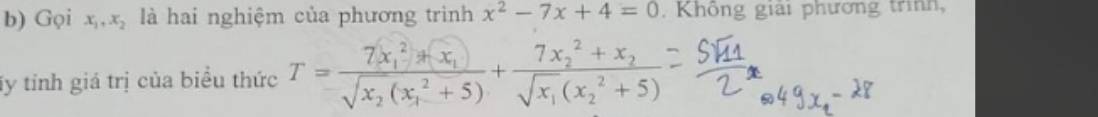Lời giải:
Áp dụng định lý Viet:
$x_1+x_2=7$
$x_1x_2=4$
Khi đó:
\(T=\frac{(x_1+x_2)x_1^2+x_1}{\sqrt{x_2}(x_1^2+5)}+\frac{(x_1+x_2)x_2^2+x_2}{\sqrt{x_1}(x_2^2+5)}\\ =\frac{x_1(x_1^2+x_1x_2+1)}{\sqrt{x_2}(x_1^2+5)}+\frac{x_2(x_2^2+x_1x_2+1)}{\sqrt{x_1}(x_2^2+5)}\\ =\frac{x_1(x_1^2+4+1)}{\sqrt{x_2}(x_1^2+5)}+\frac{x_2(x_2^2+4+1)}{\sqrt{x_1}(x_2^2+5)}\\ =\frac{x_1(x_1^2+5)}{\sqrt{x_2}(x_1^2+5)}+\frac{x_2(x_2^2+5)}{\sqrt{x_1}(x_2^2+5)}\\ \)
$=\frac{x_1}{\sqrt{x_2}}+\frac{x_2}{\sqrt{x_1}}$
$=\frac{(\sqrt{x_1}+\sqrt{x_2})(x_1-\sqrt{x_1x_2}+x_2)}{\sqrt{x_1x_2}}$
$=\frac{(\sqrt{x_1}+\sqrt{x_2})(7-\sqrt{4})}{\sqrt{4}}$
$=\frac{5}{2}(\sqrt{x_1}+\sqrt{x_2})$
$=\frac{5}{2}\sqrt{x_1+x_2+2\sqrt{x_1x_2}}$
$=\frac{5}{2}\sqrt{7+2\sqrt{4}}=\frac{5\sqrt{11}}{2}$