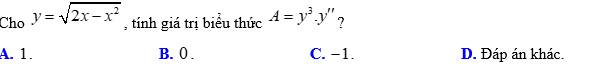7 tháng 5 lúc 20:03
\(y=\sqrt{2x-x^2}\)
=>\(y'=\dfrac{\left(2x-x^2\right)'}{2\sqrt{2x-x^2}}=\dfrac{2-2x}{2\sqrt{2x-x^2}}=\dfrac{1-x}{\sqrt{2x-x^2}}\)
\(y''=\dfrac{\left(1-x\right)'\cdot\sqrt{2x-x^2}-\left(1-x\right)\cdot\left(\sqrt{2x-x^2}\right)'}{2x-x^2}\)
=>\(y''=\dfrac{-\sqrt{2x-x^2}+\left(x-1\right)\cdot\dfrac{1-x}{\sqrt{2x-x^2}}}{2x-x^2}\)
\(=\dfrac{-\left(2x-x^2\right)+\left(x-1\right)\left(1-x\right)}{\sqrt{2x-x^2}\left(2x-x^2\right)}\)
\(=\dfrac{-2x+x^2+1-x^2}{\sqrt{2x-x^2}\left(2x-x^2\right)}=\dfrac{-2x+1}{\sqrt{2x-x^2}\left(2x-x^2\right)}\)
\(y^3\cdot y''=\dfrac{-2x+1}{\sqrt{2x-x^2}^3}\cdot\sqrt{2x-x^2}^3=-2x+1\)
=>Chọn D
Đúng 3
Bình luận (0)
