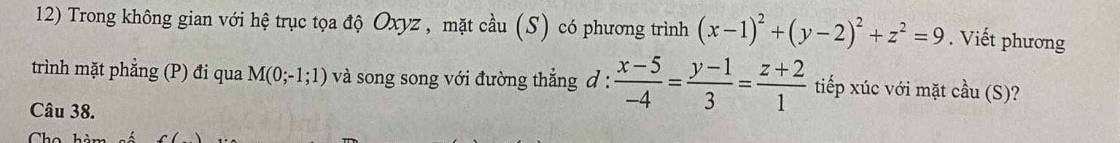Gọi pt (P) dạng \(ax+by+cz+d=0\) (với a;b;c ko đồng thời bằng 0)
Do (P) song song d nên:
\(-4a+3b+c=0\) \(\Rightarrow c=4a-3b\)
Do (P) qua M nên: \(-b+c+d=0\) \(\Rightarrow-b+4a-3b+d=0\)
\(\Rightarrow d=-4a+4b\)
\(\Rightarrow\left(P\right):ax+by+\left(4a-3b\right)z-4a+4b=0\)
Mặt cầu (S) tâm \(I\left(1;2;0\right)\) bán kính \(R=3\)
(P) tiếp xúc (S) \(\Rightarrow d\left(I;\left(P\right)\right)=R\)
\(\Rightarrow\dfrac{\left|a+2b-4a+4b\right|}{\sqrt{a^2+b^2+\left(4a-3b\right)^2}}=3\)
\(\Leftrightarrow\left(a-2b\right)^2=17a^2+10b^2-24ab\)
\(\Rightarrow\left[{}\begin{matrix}4a=3b\\2a=b\end{matrix}\right.\)
Chọn \(\left(a;b\right)=\left(3;4\right);\left(1;2\right)\)
\(\Rightarrow\left(P\right):ax+by+\left(4a-3b\right)z-4a+4b=0\)
Có 2 mp thỏa mãn: \(\left[{}\begin{matrix}3x+4y+4=0\\x+2y-2z+4=0\end{matrix}\right.\)